一、单因素完全随机设计

问题引入中学校主要是进行教材实验，四种不同版本的教材在随机的在四个班实施，教材是自变量。像这样的实验中的自变量称为因素。只有一个自变量的实验称为单因素实验，有两个或两个以上自变量的实验称为多因素实验。教材这个因素有四种版本，称为因素的水平。问题引入中的实验就是单因素实验。如果要研究两种教学方法在理解力不同的三个小组中的实验效果是否有显著性差异，这一实验设计就是双因素实验设计，教学方法和理解力是两个因素，前者有两种水平，后者有三种水平。对以上各种实验效果进行显著性检验，就要用方差分析。对只包括一个自变量的分析是单因素方差分析，有两个或两个以上自变量的方差分析是多因素方差分析。

在实验中只有一个实验因素，这个因素被分成k（k>2）种不同的水平，将n名被试随机地分成k个实验组，每个实验组被随机地指定接受一种实验处理，如问题引入中的教材实验，这种实验设计就是单因素完全随机设计。对这一实验结果的分析，称为单因素完全随机设计的方差分析。这样的分析在教育实践中很普遍，如比较三种记忆方式在记忆同一内容时的效果是否有显著性差异的实验设计；研究学生成绩时，同一年级不同班级的考试成绩是否有显著性差异等。

二、单因素完全随机设计方差分析的方法

求平方和是方差分析中很关键的一步。在实际应用中，为了计算简便和获得较为精确的结果，往往用原始观测值直接求平方和。只要根据，把用各离差求平方和的公式展开并整理即可得：

，

 

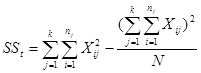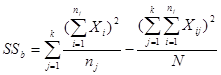
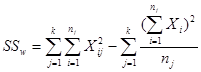
为了方便，角标可以不写出。如果设为所有观测值总和，为第个样本的观测值之和，则平方和的计算公式可简化为：

， ，

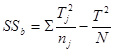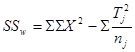
式中，为各观测值的平方之和；为观测值总和，为第个样本的观测值之和，为第个样本的容量；为观测值总数目

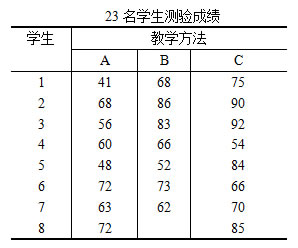
如某小学校长为改进教学方法，从一年级中随机抽取23名学生，分成三组，进行三种教学方法实验。一学期后进行统一测验。问三种教学方法的教学效果有无显著性差异？已知成绩总体服从正态分布，方差齐性。

解：提出假设。H0：==，H1：至少有一对平均数不等

求平方和。

 

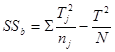
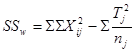
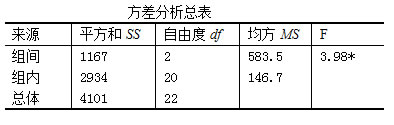
求自由度和均方。dfb=k-1=3-1=2，dfw=N-k=23-3=20，dft=N-1=23-1=22

，

求F值。=

确定α水平及F临界值。取α=0.05，df=(2,20)时，F0.05=3.49

由于计算的F=3.98>F0.05=3.49，P<0.05，所以在0.05水平拒绝原假设，接受备择假设。结论为三种教学方法的教学效果间差异显著，教学方法这个因素影响学生的学习成绩。