问题引入中的例子，通过F检验，发现差异显著，但并不意味着每对平均数之间都有差异，而是至少有一对平均数不等。那么究竟是哪对平均数不等呢？这就需要进行平均数间的多重比较，以判断哪种教材效果更显著，常用的是t检验法。

t检验法也称为最小显著性差异法，计算公式为：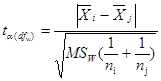

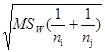式中，、为分别要比较的任意两平均数；为组内均方；、分别为要比较的两样本容量； 为自由度为时的值；为标准误。

如果设任意两平均数间差异为D，则任意两平均数间差异达到某一显著性水平的最小差异界限值为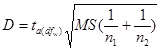：。即任意两平均数间的差异只要达到或超过一定α水平下的最小差异界限值，则认为这两个平均数在此水平上差异显著。具体判断规则为：

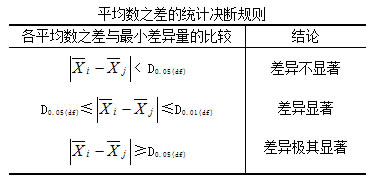
如某中学为考察四位生物教师的教学效果是否一样，从四位教师所任课的四个班级中分别随机抽取5名学生的生物成绩。问这四位教师的教学效果是否有显著性差异？如果有差异，检验哪对差异显著。已知生物成绩服从正态分布，方差齐性。

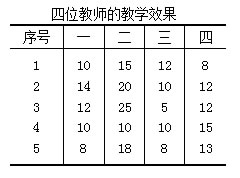
解：H0：===；H1：至少有一对平均数不等。

由于T=54+88+45+60=247，N=20，=102+142+……+132=3457，所以

，

  

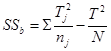
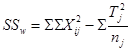
dft=N-1=19，dfb=k-1=3，dfW=N-k=16

（3）计算F值。

（4）选取α水平并统计决断。

取α=0.01，查F分布表，得F0.01（3，16）=5.29。由于计算的F=5.508> F0.01（3，16）=5.29，P<0.01，所以拒绝原假设，接受备择假设。结论为：四位教师的教学效果有极其明显的差异。

各平均数间的多重比较。其步骤为：

（1）求各样本平均数。

，，，

（2）求最小差异的界限值。查t分布表，当dfw=16时，t0.05(16)2.12，t0.01(16)=2.921。又因

，因此

，

（3）列出平均数多重比较表，表内为任意平均数间差异的绝对值。

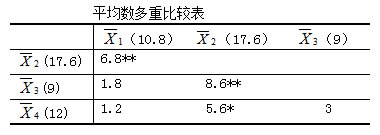
（4）把每两个平均数间的差值与最小临界值进行比较。第二个样本平均数与第一、第三个样本间均达到非常显著的差异，所以在差值的右上方标**，与第四个平均数达到了显著性差异，在差值的右上方标*，说明第二位生物教师的教学效果要好于其他三位教师。