一、相关的概念

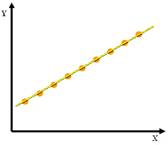
设有两个变量X和Y ，变量Y随变量X一起变化，当X取某个数值时，Y依确定的关系取相应的值，则称Y是X的函数，记为Y= f (X)。这种关系为函数关系，如左图所示。

 

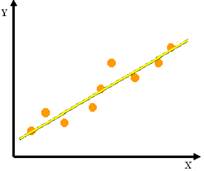
在教育实践中，教师教学质量与教师的职业认同感之间有关系，教师职业认同感越高，对教学工作越热爱，教学质量可能会越好，但高认同感并不一定带来高的教学质量；同样认同感的不同教师，教学质量也不一定一样。学生的学业成就与家庭背景、学生学业成就与教师语言表达艺术等之间也是这样的关系。像这样的关系称之为相关关系。对于相关关系，一个变量的取值不能由另一个变量唯一确定，当变量X取某个值时，变量Y的取值可能有几个，如图所示。

相关是指事物或现象间存在着一定的相互关系。如人的收入水平与受教育程度有关，教师的工作士气与管理人员的工作方式有很大相关，学生辍学与否同教学内容有一定的相关等等。统计学中的相关是指具有相关关系的不同现象之间的关系程度。依据各种现象的测量值研究各种现象间关系的密切程度，统计上叫做相关分析。

二、相关种类

1．依据相关因素的多少，可分为简相关和复相关。

分析儿童的语言表达能力与家庭环境之间的相关、学生学习成绩与智力水平间的相关等，像这样研究两个变量间的相关称为简相关。学生的学习成绩除受智力影响外，还受到教师的教学态度、学生的学习态度、学习习惯、家庭环境等因素的影响，像这样研究两个以上变量间的相关就是复相关。本章所研究的相关都是简相关。

2．依据变量分布的形态，可分为直线相关和曲线相关。

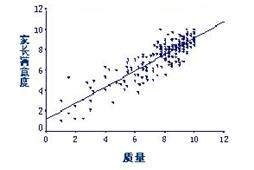
直线相关的各变量，其变化的趋势是稳定的，如家长对学校的满意度与学校教育质量。如果两个变量有直线关系（拟合直线），则由两变量成对观测值描的点呈直线趋势。曲线相关的各变量，其变化程度和趋势都是不稳定的，即当一种变量有较大增加时，另一种变量不总是有较大增加；或者一变量增加，另一变量先增加，后减少，前后变化不一致。若两变量呈曲线关系，则由两变量成对观测值描的点呈曲线趋势。

本章所研究的相关，是简相关中的直线相关。

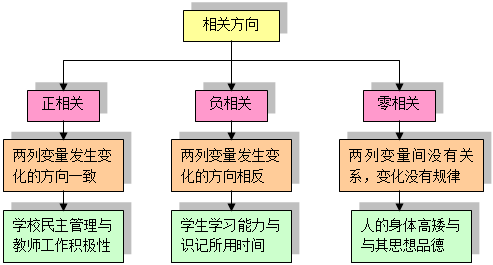
3．按变量变化的方向，可分为正相关、负相关和零相关。

 

 

三、相关散布图

分析像学生学业成就与智商之间的关系程度，可以直接绘制相关散布图来判断。相关散布图是指在直角坐标系中，以横轴表示X列变量，以纵轴表示Y列变量，以零点为原点，依据两个变量成对观测值在直角坐标系内描的点所形成的图形。各种相关关系，可以通过绘制相关散布图来直观、形象地显示两变量之间的相关关系。下图是各种相关散布图。

    

   

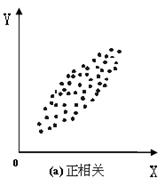
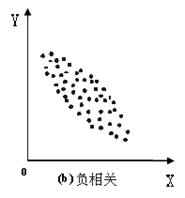
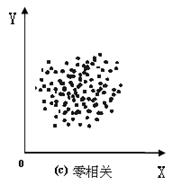
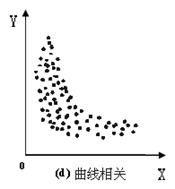
通过上面各种相关的散布图，我们可以发现，运用相关散步图：

第一，可以判断相关是否直线式。当两变量相关散布图是椭圆形，这说明两变量之间是直线相关，如图(a)；当两变量相关散布图呈弯月状，说明两变量之间是非线性关系，如图(d)。

第二，判断相关密切程度高低。散布图的椭圆形状较为狭长，表示两列变量间相关程度较高；如果椭圆形状比较粗，表示两列变量间是低相关。

第三，判断相关变化方向。

四、相关系数

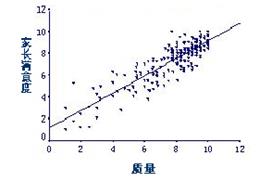
我们通过家长对学校的满意度与学校教育质量关系的相关散布图，可以发现二者之间是正相关，相关程度很高，但高到什么程度呢？如果要精确了解变量间的相关程度，需要求出描述变量间相关程度的量数。相关系数是描述两个变量间相关程度与变化方向的数量表现形式，表明变量间相互伴随变化的趋势。总体相关系数用（读rho）表示，样本相关系数用符号表示。

在教育研究和教育管理中，解释和应用相关系数要注意以下问题：

第一，相关系数的取值范围是-1≤≤1，一般取小数点后两位。的正负号表明两变量间变化的方向，无大小意义；的绝对值大小表明两变量间相关的程度。如=0.72与=-0.72，两者相关方向相反，但相关程度相同。的绝对值越接近1，表示两变量间相关程度越高，=1时，表示完全相关，但这在教育实践中几乎是不可能的。

第二，强相关意味着两个变量之间有密切关系，但不一定是因果关系。

第三，相关系数是一个比值，不是等距的测量单位。因此，在比较相关程度时，不能用倍数关系说明，不能做加、减、乘、除运算。如=0.25，=0.5，=0.75，我们不能说与、与r3的相关程度之差是相等的，也不能认为是的两倍。

第四，相关系数受变量取值区间大小及观测值个数的影响较大。因此，在研究现象间相关关系时要获得足够的观测值，一般要求大样本。在比较两相关系数大小时，也必须考虑到观测值数目上的差异。本章所举例题，只列少数成对观测值，只是为了说明计算方法时方便。

第五，通过实际观测值计算的相关系数，须经过显著性检验确定其是否有意义。在相关系数有意义的前提下，一般根据下表对其进行解释：

的取值与相关程度