第七章 相关分析
 知识点二:积差相关
知识点二:积差相关
一、积差相关的概念与适用条件
积差相关是20世纪初由英国统计学家皮尔逊提出的,亦称皮尔逊相关法。它是研究两变量间直线相关方向和程度最基本、最常用的方法,基本公式为:
![]()
式中,![]() 、
、![]() 分别为X变量和Y变量的离差;
分别为X变量和Y变量的离差;![]() 、
、![]() 分别为X变量和Y变量的标准差;N为成对观测值的个数。
分别为X变量和Y变量的标准差;N为成对观测值的个数。
积差相关系数主要适用于以下情况:
第一,必须是成对观测值,且一般不能少于30对数据。如果数据太少,由于误差影响,虽可计算出一个相关系数,但与实际不符,使相关系数失去意义。
第二,两列变量各自总体分布服从正态,或接近正态的单峰对称分布(如果没有特殊说明,总体都服从正态分布)。
第三,两列变量都是连续变量且两列变量之间是线性相关。判断两列变量是否是线性相关可作相关散布图进行初步分析。
二、积差相关的计算方法
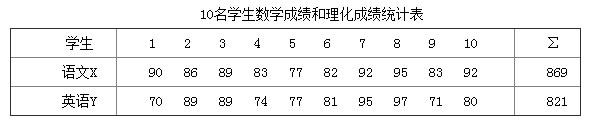
问题导入中学生数学成绩与理化成绩是连续变量,总体服从正态分布,因此采用积差相关分析两科之间的相关性。
用基本公式法计算相关系数非常麻烦,把![]() 进行转化,得到:
进行转化,得到:
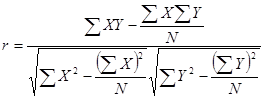
式中,![]() 为积差相关系数;X、Y分别为两变量的原始观测值;N为观测值的对数
为积差相关系数;X、Y分别为两变量的原始观测值;N为观测值的对数
把观测值直接带入计算公式就可以求得相关系数,计算求得数学测验成绩与理化测验成绩之间的相关系数r =0.56。
利用原始数据求积差相关系数的步骤为:
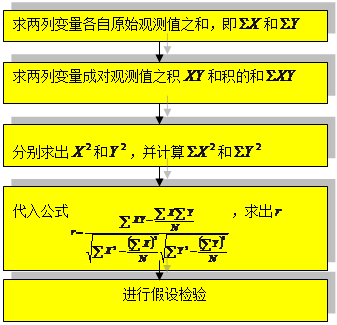
三、积差相关系数的假设检验
问题导入中数学成绩与理化成绩的相关系数为0.56,那么是不是说明数学成绩与理化成绩的相关程度就是0.56呢?这需要对r =0.56进行假设检验以确定其是否有意义,即检验所求得的相关系数![]() 与
与![]() =0(总体相关系数)之间是否有显著性差异。如果差异显著,则说明计算的
=0(总体相关系数)之间是否有显著性差异。如果差异显著,则说明计算的![]() 有意义。否则,即使
有意义。否则,即使![]() 值很大,也是由抽样误差造成的。
值很大,也是由抽样误差造成的。
(一)总体相关系数的显著性检验
由于样本相关系数![]() 的抽样分布随着总体相关系数
的抽样分布随着总体相关系数![]() 和样本容量
和样本容量![]() 的大小而变化。当
的大小而变化。当![]() =0时,样本
=0时,样本![]() 的抽样分布是对称的,大样本时
的抽样分布是对称的,大样本时![]() 服从正态分布,小样本时
服从正态分布,小样本时![]() 服从
服从![]() 分布;当
分布;当![]() ≠0时,样本
≠0时,样本![]() 的抽样分布一般为偏态。因此,在实际推断时,常根据原假设
的抽样分布一般为偏态。因此,在实际推断时,常根据原假设![]() =0和
=0和![]() ≠0两种情况分别采取不同的检验方法。
≠0两种情况分别采取不同的检验方法。
1.原假设为![]() :
:![]() =0,直接查表法。
=0,直接查表法。
直接查积差相关系数临界值表。在一定![]() 水平下,
水平下,![]() =
=![]() -2时对应的表中
-2时对应的表中![]() 就是判断能否拒绝
就是判断能否拒绝![]() 的临界值。如果计算的
的临界值。如果计算的![]() 值大于或等于
值大于或等于![]() 值,则拒绝原假设,说明样本相关系数与零相关有显著差异,相关系数有意义,否则保留原假设,说明样本来自一个零相关的总体。比如问题导入中r =0.56,n=10,所以df=n-2=8,当α=0.05时,
值,则拒绝原假设,说明样本相关系数与零相关有显著差异,相关系数有意义,否则保留原假设,说明样本来自一个零相关的总体。比如问题导入中r =0.56,n=10,所以df=n-2=8,当α=0.05时,![]() =0.632。由于计算的r =0.56<
=0.632。由于计算的r =0.56<![]() =0.632,所以P>0.05,接受原假设,即r =0.56与
=0.632,所以P>0.05,接受原假设,即r =0.56与![]() =0差异不显著,说明学生的数学成绩与理化成绩相关不显著。
=0差异不显著,说明学生的数学成绩与理化成绩相关不显著。
从这一检验结果我们也会发现,相关分析必须大样本。根据小样本观察值可能会计算出较大的相关系数,但由于样本太小,误差太大,计算结果主要是抽样误差造成的。
2.原假设为![]() ≠0
≠0
如果![]() ≠0,而是某一数值,即
≠0,而是某一数值,即![]() =c(c为常数)时,
=c(c为常数)时,![]() 的抽样分布呈偏态。在这种情况下,可将
的抽样分布呈偏态。在这种情况下,可将![]() 值经过一定的公式转换为
值经过一定的公式转换为![]() 值(查相关系数r值的
值(查相关系数r值的![]() 转换表)。由于
转换表)。由于![]() 服从正态分布,所以可以采用Z检验,公式为:
服从正态分布,所以可以采用Z检验,公式为: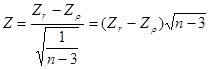
式中,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的正态转换值,
的正态转换值,![]() 为样本观测值的对子数。
为样本观测值的对子数。
如问题导入中求得数学成绩与理化成绩的r =0.56,而原有的研究表明学生数学学习与理化成绩之间的相关程度为0.65。问现在的研究结果与原来的结果一致吗?
解: H0:ρ=0.65,H1:ρ≠0.65
当![]() =0.56时,
=0.56时,![]() =0.633,
=0.633,![]() =0.65时,
=0.65时,![]() =0.775
=0.775
![]() -0.376
-0.376
根据题意,采用双尾检验,取α=0.05。由于计算的![]() =0.376<
=0.376<![]() 0.05/2=1.96,P>0.05。所以保留原假设,认为现在求得的结果与原来的研究结果一致。
0.05/2=1.96,P>0.05。所以保留原假设,认为现在求得的结果与原来的研究结果一致。
(二)两样本相关系数间差异的显著性检验
某地区研究人的身体和体重之间的相关程度,随机抽取120名11~15岁儿童,测得其身高与体重间的相关系数为![]() =0.89;随机抽取21~25岁青年124名,测得其身高与体重间的相关系数为
=0.89;随机抽取21~25岁青年124名,测得其身高与体重间的相关系数为![]() =0.72,然后该地区认为儿童的身高与体重的相关程度高于青年的身高与体重的相关程度。这一结论正确吗?
=0.72,然后该地区认为儿童的身高与体重的相关程度高于青年的身高与体重的相关程度。这一结论正确吗?
判断结论正确与否,主要是检验![]() =0.89与
=0.89与![]() =0.72二者所来自的总体相关程度是否有差异,这就是两个样本相关系数间差异的检验。将r转换为
=0.72二者所来自的总体相关程度是否有差异,这就是两个样本相关系数间差异的检验。将r转换为![]() 后采用Z检验,公式为
后采用Z检验,公式为
![]()
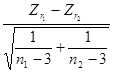
式中:![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的正态转换值;
的正态转换值;![]() 、
、![]() 分别是两样本的容量。
分别是两样本的容量。
解:![]() :
: ![]() ,
, ![]() :
: ![]()
查相关系数r值的![]() 转换表,将r转换为
转换表,将r转换为![]() :当
:当![]() =0.89时,
=0.89时,![]() =1.42192;
=1.42192; ![]() =0.72时,
=0.72时, ![]() =0.90764。
=0.90764。
已知![]() =120,
=120, ![]() =124。得
=124。得
Z =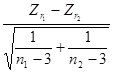 =
=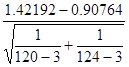
=3.97
取α=0.01,则![]() =2.58。由于计算的Z=3.97>2.58, P<0.01,所以拒绝原假设,认为这两个年龄段的身高与体重间的相关程度差异是非常显著的。因此他们的研究结论是正确的。
=2.58。由于计算的Z=3.97>2.58, P<0.01,所以拒绝原假设,认为这两个年龄段的身高与体重间的相关程度差异是非常显著的。因此他们的研究结论是正确的。
