第七章 相关分析
 知识点三:等级相关
知识点三:等级相关
一、等级相关的概念
这一问题的解决,就如问题导入中提出的那样,如果把10名学生的成绩以等级次序排列是否可以进行相关分析?获取的数据是等级变量,就采用等级相关法。事实上,教育实践中许多现象不能用连续变量来表示,如学生思想品德的水平、学习习惯的好坏、学校办学水平的高低、教师教学能力的高低等, 常常用等级来表示。另外,当前在义务教育阶段学生的各科学业成绩也倡导采用等级制。
等级相关是指以等级次序排列的两列或两列以上变量之间的相关。用等级相关法研究多变量之间的关系时,不受变量总体分布形态的限制,只考虑变量的位置而不问其数量的大小。因此,等级相关既适用于具有等级特征的资料间的相关分析,也适用于虽是测量数据但个数较少或不符合正态分布情况下的相关分析。常用的等级相关方法主要有斯皮尔曼等级相关和肯德尔和谐系数。
二、斯皮尔曼等级相关
由于小学生作文能力与阅读能力是两列等级变量,其等级相关分析需要采用斯皮尔曼等级相关。斯皮尔曼等级相关是由英国统计学家斯皮尔曼(Charles Spearman)提出的,是指两列以次序排列的等级变量间的相关。斯皮尔曼等级相关系数用符号![]() 表示,计算公式为
表示,计算公式为
![]() =
=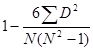
式中,![]() 为斯皮尔曼等级相关系数;D为两列变量每对数据等级之差;N为等级数据的对子数
为斯皮尔曼等级相关系数;D为两列变量每对数据等级之差;N为等级数据的对子数
斯皮尔曼等级相关主要适用于:1)两列变量的资料为等级变量,且具有线形关系;2)两列连续变量按大小顺序排列成等级;3)不要求总体服从正态或单峰对称分布。
计算斯皮尔曼等级相关系数的步骤为

下面分析小学生作文能力与阅读能力之间的相关程度。
10名小学生作文能力与阅读能力等级相关计算表
学生 |
清楚X |
流利Y |
D(X-Y) |
D2 |
1 2 3 4 5 6 7 8 9 10 |
2 3.5 3.5 6 10 8 9 7 5 1 |
1 6.5 4 8 9 5 10 6.5 2 3 |
1 -3 -0.5 -2 1 3 -1 0.5 3 -2 |
1 9 0 4 1 9 1 0.25 9 4 |
Σ |
|
|
|
38.25 |
代入公式得:![]() = 1-
= 1-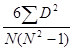 =1-
=1-![]() =0.77
=0.77
即小学生的作文能力与阅读能力等级之间的相关系数是0.77。![]() =0.77是否有意义呢?需要进行相关系数的假设检验。对等级相关系数
=0.77是否有意义呢?需要进行相关系数的假设检验。对等级相关系数![]() 的显著性检验,其假设为:
的显著性检验,其假设为:![]() :
:![]() =0 ,
=0 , ![]() :
:![]() ≠0。检验时,直接用
≠0。检验时,直接用![]() 与一定α水平下的等级相关系数显著性临界值比较,以确定
与一定α水平下的等级相关系数显著性临界值比较,以确定![]() 是否有意义,或者说
是否有意义,或者说![]() 是否来自零相关的总体。
是否来自零相关的总体。
求得的![]() =0.77,N=10,取α=0.01,查斯皮尔曼等级相关系数显著性临界值,当n=10时,界限值为0.746。由于计算的
=0.77,N=10,取α=0.01,查斯皮尔曼等级相关系数显著性临界值,当n=10时,界限值为0.746。由于计算的![]() =0.77>0.746,P<0.01,所以拒绝原假设,
=0.77>0.746,P<0.01,所以拒绝原假设,![]() =0.77有意义,二者之间高度相关。
=0.77有意义,二者之间高度相关。
如果资料本是连续变量,而观测值个数较少或总体不服从正态分布,这时首先把连续变量转化为等级变量,然后用斯皮尔曼等级相关描述其相关程度。
下面是10名初二学生期中考试的代数成绩(X)和期末考试的代数成绩(Y),试用等级相关法描述期中代数成绩与期末代数成绩之间的相关程度。
10名初二学生期中、期末代数成绩表
学生 |
期中 |
期末 |
|
|
|
|
1 2 3 4 5 6 7 8 9 10 |
90 75 72 87 65 73 81 72 68 58 |
87 76 73 80 60 74 85 75 65 60 |
1 4 6.5 2 9 5 3 6.5 8 10 |
1 4 7 3 9.5 6 2 5 8 9.5 |
0 0 -0.5 -1 -0.5 -1 1 1.5 0 0.5 |
0 0 0.25 1 0.25 1 1 2.25 0 0.25 |
Σ |
|
|
|
|
|
6 |
列相关系数计算表。首先将连续变量转换为等级变量,然后再在求出![]() 和
和![]() ,最后带入公式:
,最后带入公式:![]() = 1-
= 1-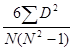 =1-
=1-![]() =0.96
=0.96
取α=0.01,查斯皮尔曼等级相关系数显著性临界值,当n=10时,界限值为0.746。由于计算的![]() =0.96>0.746,P<0.01,所以拒绝原假设,
=0.96>0.746,P<0.01,所以拒绝原假设,![]() =0.96有意义,二者之间极高相关。
=0.96有意义,二者之间极高相关。
三、肯德尔和谐系数
下面是某校6位领导者对7位教师年终考核的评定成绩,问6位领导对7名教师的评定等级是否一致?
6位领导对7位教师的评定等级
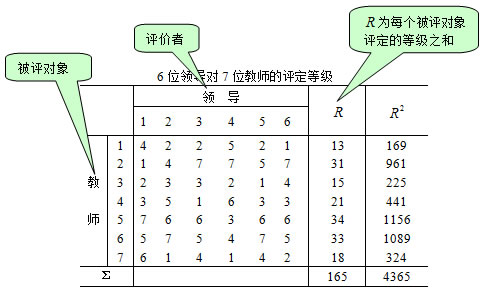
分析6位领导对7名教师的评定等级是否一致,就是分析6为领导在评定时把握的标准是否一致。像这样的描述三个或三个以上等级变量间的一致性程度,要用肯德尔和谐系数,又叫肯德尔W系数。它常用来表示![]() 个评定者对
个评定者对![]() 个对象进行等级评定的一致性程度或同一个评定者对
个对象进行等级评定的一致性程度或同一个评定者对![]() 个对象先后评定
个对象先后评定![]() 次,其等级之间的一致性程度,所以,又叫评分者信度。肯德尔和谐系数用符号W表示,计算公式为:
次,其等级之间的一致性程度,所以,又叫评分者信度。肯德尔和谐系数用符号W表示,计算公式为: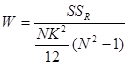
式中,![]() ,为
,为![]() 的离差平方和;
的离差平方和;![]() 为每个被评对象评定的等级之和;
为每个被评对象评定的等级之和;![]() 为被评定对象的个数;
为被评定对象的个数;![]() 为评定者个数
为评定者个数
从公式可以看出, W值是非负数,取值范围是![]() 。对于相关的方向,要依据实际资料进行分析。
。对于相关的方向,要依据实际资料进行分析。
![]() 的大小反映了几个评定者对若干个对象评定等级的一致性程度。评价者对每位评价对象评定等级差异较大,各被评对象分别获得的等级总和差异就很小,肯德尔和谐系数就小,评定者意见很不一致;反之,评价者评定等级越一致,各被评对象分别获得的等级总和差异就越大,肯德尔和谐系数就越大,评定者意见就越一致。
的大小反映了几个评定者对若干个对象评定等级的一致性程度。评价者对每位评价对象评定等级差异较大,各被评对象分别获得的等级总和差异就很小,肯德尔和谐系数就小,评定者意见很不一致;反之,评价者评定等级越一致,各被评对象分别获得的等级总和差异就越大,肯德尔和谐系数就越大,评定者意见就越一致。
这时求肯德尔和谐系数的步骤为:
已知N =7 ,![]() =6,带入公式得
=6,带入公式得![]()
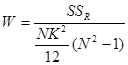 =
=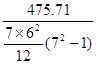 =0.47
=0.47
当3≤N≤7时,检验肯德尔W系数是否显著可直接查W系数临界表,按照一定α水平及K和N的数目,在表中找到其对应的![]() 值,用实际求得的
值,用实际求得的![]() 与
与![]() 值比较。如果实际求得的
值比较。如果实际求得的![]() >
>![]() ,则说明W系数达到一定的显著性水平,认为各评价者的意见比较一致;否则认为各评价者的意见不一致,求得的W系数值无意义。
,则说明W系数达到一定的显著性水平,认为各评价者的意见比较一致;否则认为各评价者的意见不一致,求得的W系数值无意义。
对W=0.47进行检验。查肯德尔和谐系数显著性临界值表,N =7,![]() =6时,取α=0.01,界限值为422.6。由于计算的
=6时,取α=0.01,界限值为422.6。由于计算的![]() >422.6,P<0.01,所以拒绝原假设,6位领导对7位教师年终考核评定一致性程度为W=0.47。
>422.6,P<0.01,所以拒绝原假设,6位领导对7位教师年终考核评定一致性程度为W=0.47。
当N>7时,用![]() 检验(此方法在假设检验中学习),
检验(此方法在假设检验中学习),![]() = K (N-1)W(df =N-1)
= K (N-1)W(df =N-1)
