一、判断正误

1.×；2.×；3.√；4.×；5.√；6.×；7.√；8.×；9.√；10.×

二、单项选择

1.C；2.B；3.A；4.C；5.A；6.D；7.D；8.A；9.A；10.B

三、简答与计算

1．确定测验的目的；确定测验的属性；明确测验的性质和用途；明确测验对象；分析测验目标

2．第一，能评估特定地区、特定学校乃至特定班级的学生在特定课程、特定时间内进步的程度。第二，在编制和组织方面省时、省力、灵活和方便，编制相对容易。第三，与教材内容联系紧密，针对性强。第四，可根据教学需要，随时安排测试。

3. >，P<0.05，差异显著

4．H0：=，H1：≠；

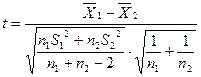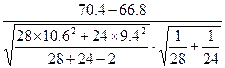==1.26

由于计算的t=1.26< t0.05/2（50）=2.01，所以接受原假设，说明“男生”与“女生”在平均分上的差异主要是由于抽样误差造成的，即“男生”与“女生”的真实水平并无差异。所以，在教学中认为男生数学水平比女生数学水平高的看法是片面的、缺乏科学依据的。

5. 算术平均数为77，=7.509分。

四、论述与计算

1．答案要点

第一，每道试题测量的应是重要的学习结果，而非细枝末节的内容。

第二，题干意义完整并能表达一个确定的问题。

第三，题干中避免滥用否定结构，尽可能采用正面叙述。

第四，题干要简练。

第五，备选答案中的干扰项应具有似真性。

第六，注意避免某种暗示或特殊限定词。

第七，正确答案的位置应随机排列。

第八，选项文字表述力求简短，避免选项含有相同的字词。

2．解：提出假设。H0：===，H1：至少有一对平均数不等。