人的许多心理特质如智力、技能等，是随着时间以有规律的方式发展的，所以可将个人的成绩与各种发展水平的人的平均表现相比较。根据这种平均表现所制成的量表就是发展常模。常见的发展常模有发展顺序量表、智力年龄、年级当量等。

（一）发展顺序量表

根据发展性常模制定出来的量表称为发展量表。个人在发展量表中的成绩可以明确指出他的某一心理特质在正常发展途径中处于怎样的发展水平。常见的发展量表有比奈-西蒙智力量表、斯坦福-比奈量表等。

发展量表以个人的发展阶段为单位来报告测验分数，因此测验分数易于被人理解。比如说，如果仅报告个体在某一智力测验中得分为100分，那么即使知道该测验满分为多少，仍然不能明确获得个体智力发展水平的信息。然而，以个人发展至某一阶段的形式来报告分数，如个体的智力水平相当于9岁儿童的平均水平，则能够比较清楚地描述个体的发展状况。同时，这一分数又可以与同等团体做直接比较，为个人的纵向比较和横向比较均提供了基础，因而发展量表曾被广泛应用在心理测量和教育评价领域上。但发展量表的使用也有局限，主要体现在以下几点：

（1）发展量表的编制基础在于所测量的心理特质随时间（如年龄、年级）发生系统变化的情况，这就决定了发展量表仅适用于测量在一定年龄范围内随时间而有系统地改变的心理特质（如智力），而不适用于测量与发展无关的特质（如视力）。

（2）发展量表的编制基础同时也决定了绝大部分发展量表仅适用于尚在发展中的儿童和青少年，对于各种心理特质相对稳定的成人并不适用。

（3）个人的心理和行为发展受到教育与经验的影响，因而发展量表只适用于典型环境下成长的个人。

（4）由于大部分心理特质在整个年龄或年级范围内的发展并不完全均衡，这就导致发展量表往往并非等距量表；也就是说，发展量表的单位并不是恒定相等的。比如说，四年级两个月（例如，从4-2到4-4）的成就增长差别在教育上并不等价于后面年级水平两个月（例如，从8-2到8-4）的成就增长。由于年龄和年级常模错误地暗示被试能力的增长比率是每年不变的，因此教育测量专家往往不鼓励人们使用年龄和年级常模。

（5）获得同样的年龄或年级当量分数，并不一定具有相同的智力或学业水平。如一个7岁的儿童和一个9岁的儿童同得智龄8岁，虽然他们获得同样的智龄，但是年龄较小者的智力水平相对较高。

（二）智力年龄

比内-西蒙量表中首先使用智力年龄的概念。

在像比内-西蒙量表示的年龄量表中，每个题目放在大部分儿童都能成功地完成的那个年龄水平，从而把题目分成若干年龄组。如果为每个年龄水平都编制一些适当的题目，便可得到一个评价儿童智力发展水平的年龄量表。一个儿童在年龄量表上所得的分数，就是最能代表他的智力水平的年龄。这种分数叫做智力年龄，简称智龄。

求智龄的方法：

1.将儿童在测验上的分数与个年龄组的一般儿童比较，便可给以一个年龄分数。如果被试在低年龄水平题目上失败，但通过了更高年龄水平的题目。要首先算出举出年龄，然后再按月份计算，加在基础年龄上。

2.不把题目分到各年龄组。在这种情况下，首先根据被试在整个测验中正确反映的题目数或反应时间而得一原始分数，而将标准化样本中每个年龄组的平均原始分数作为年龄常模。通过将原始分数与年龄常模对比，便可求得每个人的智力。

（三）年级当量

年级当量，即年级量表，测验结果说明属哪一年级的水平，在教育成就测验中常用。

年级常模的单位通常为10个月间隔（因为有两个月的假期）。如5年级的分布为5-0到5-9。

年级当量只适用于一般课程，不适合只学1-2年的课程。

年级当量只适用于解释本学年的水平，不适用于跨学年的。如一个五年级学生的年级当量为8，并不能说他已经掌握了8年级的课程。

（一）定义

百分等级（percentile rank）是应用最广的导出分数。一个原始分数的百分等级是指一个群体的测验分数中，得分低于这个分数的人数的百分比。也就是说，如果将某一被试群体分为一百个等级，则每位被试所占的等级数就是百分等级。例如，某一被试在一项测验中得82分，经过换算，百分等级分数为75，就表示参加该项测验的人得分低于82分的占全体被试的75%，并说明超过他的成绩82分的人仅有25%，我们通常用PR 来表示百分等级。百分等级取值越大，说明成绩越优秀。

1.图解法

一种形象直观的方法是利用累加曲线来求解。所谓累加曲线，是指这样的曲线图：用横轴表示各分数（或各分组区间的组中值），用纵轴表示各分数（或各分组中值）所对应的累加频率。欲计算分数的百分等级，只需从横轴该分值处引一条与纵轴平行的直线，与累加曲线相交，交点处的纵坐标值就是的百分等级，如图3-1所示。

图3-1 用累加曲线求解百分等级

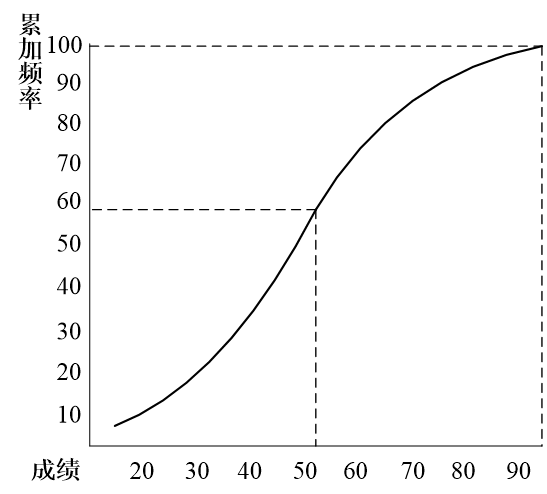
但这种求解方法极不可靠，所得结果的精确度依赖于作图的精度，在大多数情况下只是一个粗略的估计值。要想获得精确的结果，则应采用下面介绍的公式法。

2.公式法

在以下两种情况中应使用不同的公式：

（1）对于未分组数据，

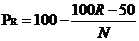（3.1）

其中，为总人数，为的排名（由高到低）。例如：某女生的英语成绩为96，在全年级300名同学中排第15位，那么该生成绩的百分等级为：

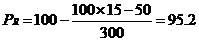
这就是说，全年级中有95.2%的同学这次英语考试的成绩不如她。

（2）对于分组数据，

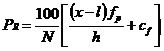（3.2）

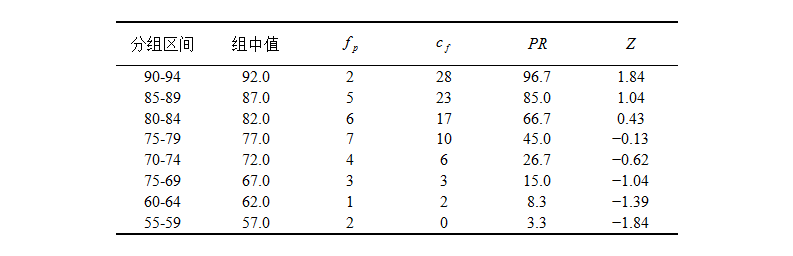
其中，为原始分数所在组的精确下限，是所在组的频数，是以下的累积频数，为组距。表3-1所示为一次语文测验的成绩分布状况，其中组中值82.0的百分等级为：

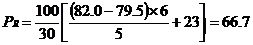
依此类推。

表3-1 一次语文测验的成绩分布（N=30）

（二）特点

1.优点

（1）百分等级是一种相对位置量数，具有可比性；

（2）具有易于计算、解释方便；

（3）易于理解，较适用于不同的对象和性质不同的测验；

（4）百分等级不受原始分数分布的影响，即使分数分布不是正态的，也不会改变百分等级常模的解释能力。

2.不足

（1）单位不等，尤其在分配的两个极端。

如果原始分数的分配是正态或近似正态分布，则靠近中央的原始分数转换成百分等级时，分数之间的差异便夸大了，对接近两极端的原始分数，百分等级反应迟钝，即使原始分数发生较大的变化，也不能引起百分等级的相应变化，使得其差异缩小了。 （2）百分等级值具有顺序性，而无法用它来说明不同的被试之间分数差异的数量。

以正态分布为例，同样是相差5个百分等级，百分等级为10和5的两个分数之间的差异较之于百分等级为50和45的两个分数之间的差异更大（如图3-2）。基于这个原因，我们无法对百分等级进行四则运算，这使得进一步的统计处理存在着困难。

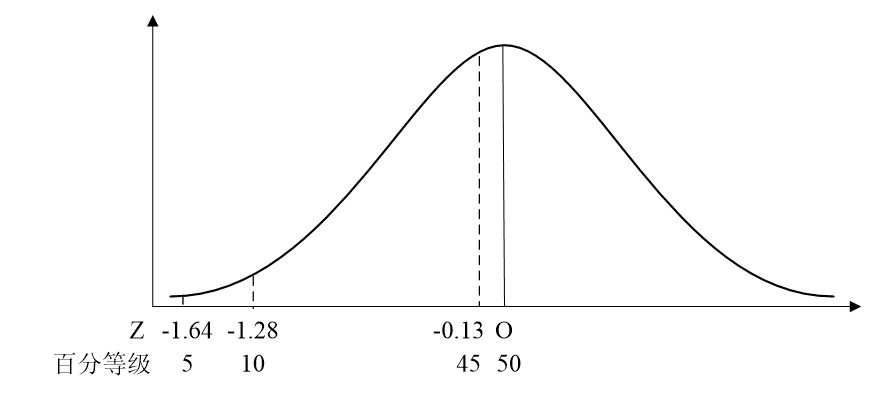
图3-2 正态分布中的百分等级

除了百分等级以外，百分位常模还包括四分位数（quartile）和十分位数（decile）。

标准分常模是将原始分数与平均数的距离以标准差为单位表示出来的量表。基本单位为标准差。常见的标准分数有：z分数，Z分数，T分数，标准九分数，利差之上（IQ）等。

标准分数可以通过线性转换，也可以通过非线性转换得到。

（一）线性转换的标准分数

Z分数

Z=（x- )/SD （3.3）

（其中X为任一原始分数，为样本平均数，SD为样本标准差。）

Z分数转换形式

Y=A+BZ （3.4）

（这里Z为转换后的标准分数，A,B为根据需要指定的常数。）

（二）非线性转换的标准分数

当原始分数不是常态分布时，也可以使之常态化，这一转换过程就是非线性的。

常态化过程计算步骤如下：

1.对每个原始分数值计算累计百分比；

2.在常态曲线面积表中，求出对应于该百分比的Z分数。

常态化标准分数也可以被转换成任何方便的形式。当以50为平均数，以10为标准差来表示时，通常叫做T分数：

T=50+10Z （3.5）

标准九分数是另一较知名的标准分数体系，其量表是个9级的分数量表，以5为平均数，2为标准差，最早时广泛应用于美国空军和某些教学情境中的分级。

其他：标准十分和标准二十分。

（一）比率智商

IQ=100（MA/CA） （3.6）

IQ：智商，MA：心理年龄，CA：实际年龄

其中MA 表示心理年龄，也就是智龄；CA表示实际年龄。在年龄量表中，我们根据某儿童正确答对的题数算出他的智龄，我们无法预先知道了他的实足年龄，这样就可根据以上公式算出他的智商。例如，一个8岁的男孩，他的实龄是8岁，若他的智龄是7岁，那么他的智商是87；若他的智龄是8岁，那么智商就是100；若智龄是9岁，他的智商就是则是112。

比率智商提出后，普遍被心理学界和医学界所接受。但由于个体智力增长是一个又快到慢再到停止的过程，即心理年龄与实足年龄并不同步增长，所以比率智尚并不适合于年龄较大的被试；另外，由于不同年龄组儿童的比率智商分布的情况是不一样的，因而相同的比率智商分数在不同年龄就具有不同的意义。

总的说来，比率智商存在的问题有：

1．第一个问题就是在计算高年龄组儿童的智商时是否应该用实际年龄作为除数，尚无一定的结论。推孟在1966年用16岁为求成人智商的除数，1937年修订的斯坦福-比内量表则用15岁作为求成人智商的除数。

2．第二个问题是智力的增长不是直线而是曲线，正如上面所讲的一样，因而以智龄作为发展水平的单位就不是一个等距单位，这显然给求智商带来了困难。达到高年龄组就更突出，因为从智力生长曲线上可知，智龄不等距到高年龄组就更为加剧了。为了克服这一困难，应对求智商的分母加以修正。斯坦福-比内量表（1937年修订版）曾对此加以修订。

（二）离差智商

早期的智力量表——比内-西蒙量表（1908）使用“智力年龄”（mental age）的概念来表示智力测验分数，即个体能通过哪个年龄组的题目，就认为其具有该年龄的智力水平。但这种表示智力的方法没有考虑实际年龄因素，比如智龄同为10岁，但对于实际年龄分别为8岁、10岁和15岁的儿童而言，意义大不相同。为了解决这个问题，推孟在1916年发表的斯坦福-比内量表中提出了比率智商（ratio IQ）的概念，规定智力年龄与实际年龄之比乘以100就得到智商（IQ）。但比率智商也存在缺点：由于各年龄被试群体智商分数的分布不同，同一智商分数所代表的百分等级就不同，无法进行比较。另外，伴随着发育的成熟，个体的智力上升到一定阶段便会逐渐稳定在一个水平上，此时如果用不再增长的智力年龄与继续增长的实际年龄相比，求得的IQ值就会下降，这在分数的解释上就会存在困难。

为了避免比率智商带来的麻烦，人们普遍认为应该通过与同年龄代表性样本均值相比较的方法来确定智商。韦克斯勒在他1949年发表的韦氏儿童智力量表（WISC）中首次用离差智商（deviation IQ）取代比率智商，其计算方法是先求出测验原始得分的标准分数Z，再进行线性转换：

IQ = 100 + 15Z （3.7）

在这里，离差智商的平均值之所以被界定为100，是出于在数值上与传统的比率智商保持一致的考虑。在比率智商中，当MA=CA时，IQ=100，它代表了每一年龄段个体的平均智力水平。常数15是常模团体测验分数的标准差。

从WISC开始，离差智商就成为了被广泛采用的智力分数指标。1960年修订发表的斯坦福-比内量表也引入了离差智商，它界定的平均值也为100，但标准差为16：

IQ = 100 + 16Z （3.8）

值得注意的是，如果要将从不同测验中得到的离差智商进行比较，必须要满足的条件是，离差智商的标准差须相同或相近，因为在不同的标准差条件下，相同离差智商值所对应的百分等级不同。测验手册中通常都会报告标准差。

离差智商是标准分数在智力测验领域中的应用，故具有前述标准分数的诸多优点：（1）它是一种等距量表，因而有利于进一步的统计分析；（2）能够运用正态分布表与百分等级相互转换；（3）在满足标准差相等的条件下，多个测验的分数可进行直接的比较。