信度（reliability）指的是测量结果的稳定性程度。换句话说，若能用同一测量工具反复测量同一种心理特质，则其多次测量的结果间的一致性程度就叫信度，有时也叫测量的可靠性。

一般来说，一个好的测量必须具有较高的信度，也就是说，一个好的测量工具，只要遵守操作规则，其结果就不应该随工具的使用者或使用时间等方面的变化而发生较大变化。例如：标准的钢尺是测量长度的一种好工具，只要操作方法得当，无论如何，也无论任何人去测量同一张桌子的高度，其结果应是基本一致，这说明其信度较高。不过，如果所用的是一种具有较大弹性的皮尺，则不同的人或同一个人在不同的时候去测量同一张桌子的高度，其结果必然会有较大的差异。这说明这种测量的信度不高。

当然，心理测量要比物理测量复杂，我们不太可能用同一种量表去反复测量一个人的同一种心理特质。某一种学绩测验就不能反复使用在同一批受测者身上，因为那样会使测量结果越来越好。因此，信度的定义还应寻求更实际的办法，以下就是除上面定义外的3种等价的信度的定义。

定义1：信度是一个被测团体的真分数的变异数与实得分数的变异数之比。经典测量理论认为：每一个被试所获得的实得分数（X）是由真分数（T）和测量误差（E）两个部份构成的，公式为：X = T + E。该公式表示个体的实得分数是真分数和测量误差的函数，这是针对某个个体而言。但信度是指一个测验的特性而不是某个人的分数特性。在讨论一组测验分数的特性时，可用方差代替具体分数，即实得分数方差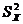（）等于真分数方差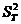（）与测量误差方差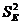（）之和，表达式为：

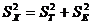（4.1）

这样，信度被界定为：一组测量分数的真分数方差与实得分数方差（总方差）的比率。其公式为：

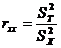（4.2）

式中代表测量的信度，代表真分数变异，代表总变异数，即实得分数的变异。

定义2：信度是一个被试团体的真分数与实得分数的相关系数的平方。

即：rxx=Ptx2（4.3）

定义3：信度是一个测验A（A卷）与它的任意一个“平行测验”a(B卷)的相关系数。即：rxx=Pxx（4.4）

在上面的定义中我们应该注意：

（1）信度指的是一组测验分数或一系列测量的特性，而不是个人分数的特性；

（2）真分数的变异数是不能直接测量的，因此信度是一个理论上构想的概念，只能根据一组实得分数作出估计。因此，定义1和定义2只具有理论意义，只有定义3才具有实际意义。

（3）描述测量一致性程度的指标还有信度指数Ptx2，通常我们用相关法，即对同一样本的测量所获得的两组测验分数的相关系数，实际上它是信度系数的平方根。

关于信度系数我们应注意：

（1）信度系数有多种，常用的信度系数有重测信度、复本信度、内部一致性系数、评分者信度等。

（2）同一种信度系数也会因样本、测查时间不同而有多个。

（3）信度系数只是对测量分数一致性的估计，但并没有指出不一致的原因。

（4）获得较高的信度只是测验有效的必要条件。

（一）反应测量过程中随机误差的大小

如果信度很低，测量的随机误差就很大，测量的结果就会与真分数发生较大偏差。而且，这种偏差完全是随机决定的，这就让人无法相信测量的结果。值得指出的是，测量中的系统误差与信度无关。因为系统误差只对测量结果产生恒定的影响，而不会使测量结果上下波动。

信度估计值可以解释为总的方差中有多少比例是由真实分数的方差决定的，也就是测验的总变异中真分数造成的变异占百分之几。例如，当rxx =0.9时，我们可以说实得分数中有90%的变异是真分数造成的，仅10%是来自测验的误差。在极端的情况下，如有rxx =1.00，则表示完全没有测量误差，所有的变异均来自真实分数；若有rxx =0.00，则所有的变异都反映的是测量误差，应该注意的是，信度系数的分布是从0.00到1.00的正数范围，代表了从缺乏信度到完全可信的所有状况。

同样，信度也可以告诉我们测量的误差比例是多少。由于信度是随情境改变的，我们就可据此精确地说明某种测验，在某种特定条件下对某种特定样本测量的误差比例是多少。

（二）评价测验

一个测验信度的高低通常用信度系数来表示，信度系数越大，测量结果越可靠。因此，信度系数是评价测验质量的一个重要指标。

信度系数的取值范围介于0.00 和1.00之间。最理想的情况是信度系数达到1.00，即两次测量结果完全一致。但实际上没有任何一个测验的信度系数能够达到1.00。那么一个测验的信度系数究竟要达到多少，测量结果才算可靠呢？在一般情况下，标准化的能力测验或学绩测验的信度系数应达到0.90以上；人格测验的信度系数应在0.80以上；教师自编学绩测验的信度应在0.60以上。测验的目的不同，对信度的要求也不同。当信度系数大于等于0.85时，测验可用于鉴别个人，也可用于团体间比较；当信度系数介于0.70和0.85之间时，测验只能用于团体间比较；当信度系数小于0.70时，测验既不能用于个人评价，也不能用于团体间的比较。

（三）解释测验分数

1．估计个体真分数的范围

我们可以利用测量标准误对个体真分数的可能范围作出估计，其公式为：

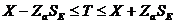（4.5）

式中，Za为该区间估计的置信度所对应的标准分数，SE为测量标准误。

若采用95%的置信度（即真分数落在所估计区间内的可能性为95%），则Za=1.96。

若采用99%的置信度（即真分数落在所估计区间内的可能性为99%），则Za=2.58。

【例4．1】 假设在一个智力测验中，某被试测量得到的IQ为110，已知该智力测验的标准差为15，信度系数为0.95，问该被试IQ真分数的可能范围是多少？

已知： X=110 =15 =0.95

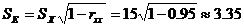
该被试的真实IQ有95％的可能性落在103（110-1.96×3.35）至117（110+1.96×3.35）区间内，也就是说，其真实IQ低于103，高于117的可能性不超过5％。

该被试的真实IQ有99%的可能性落在101（110-2.58×3.35）到119（110+2.58×3.35）区间内，也就是说，其真实IQ低于101，高于119的可能性不超过1％。

2．解释不同测验分数的差异

有时我们需要评价不同测验分数的差异，就需要进行分数差异的显著性检验。如果两个测验分数不属于同一量尺，那么来自不同测验的原始分数就不能进行直接比较，必须转换成同一量尺的导出分数（如Z分数、T分数、离差智商等）。

在统计学中，两个分数差异的标准误可表示为：

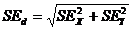（4.6）

由于两个测验的分数转换为同一量尺，所以有相同的标准差，即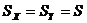

将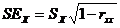和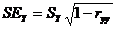代入公式4.6，得：

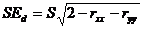（4.7）

将标准差和两个测验的信度系数代入公式（4.7），即可得到分数差异的标准误。若要在0.05显著性水平上判断两个真分数存在显著性差异，两个分数的差异应大于等于1.96SEd；若要在0.01显著性水平上判断两个真分数存在显著性差异，两个分数的差异应大于等于2.58SEd 。

【例4．2】假设用韦克斯勒成人智力量表-修订版（WAIS-R）对某被试进行测验，测得其言语智商（VIQ）为115，操作智商(PIQ)为102。已知WAIS-R的离差智商的平均数为100，标准差为15。言语量表和操作量表的分半信度系数分别为0.97和0.93。问该被试的言语智商与操作智商是否有显著差异。

已知：S=15 rxx =0.97 ryy =0.93 VIQ=115 PIQ=102

言语智商与操作智商差异分数的标准误为：

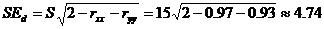
若在0.05显著性水平上判断两个真分数存在显著性差异，两个分数的差异应大于等于1.96SE d（即1.96 ×=9.29），个体在言语智商和操作智商上的分数差异至少应达到9.29分，才能达到0.05显著性水平。该被试言语智商和操作智商的分数差异为13分，超过9.29分，说明该被试言语智商和操作智商有显著差异。

若在0.01显著性水平上判断两个真分数存在显著性差异，两个分数的差异应大于等于2.58SE d（即2.58 ×4.74=12.23），该被试言语智商和操作智商的分数差异为13分，超过12.23分，说明该被试言语智商和操作智商有显著差异。