当前位置:课程学习>>第一章>>学习内容>>文本学习>>知识点四
知识点四:矢量的线性关系与矢量的分解
矢量的加法和数与矢量的乘法统称为矢量的线性运算。我们知道有限个矢量通过线性运算,它的结果仍然是一个矢量。
定义1 由矢量![]() 与数量
与数量![]() 所组成的矢量
所组成的矢量
![]() 称为矢量
称为矢量![]() 的线性组合。
的线性组合。
当矢量![]() 是矢量
是矢量![]() 的线性组合时,我们也说:矢量
的线性组合时,我们也说:矢量![]() 可以用矢量
可以用矢量![]() 线性表示。或者说,矢量
线性表示。或者说,矢量![]() 可以分解成矢量
可以分解成矢量![]() 的线性组合。
的线性组合。
我们约定,只有一个矢量与数量结合的情况,![]() 也称它为矢量
也称它为矢量![]() 的线性组合。
的线性组合。
定理1 如果矢量![]() , 那么矢量
, 那么矢量![]() 与矢量
与矢量![]() 共线的充要条件是
共线的充要条件是![]() 可以用矢量
可以用矢量![]() 线性表示,或者说
线性表示,或者说![]() 是
是![]() 的线性组合,即
的线性组合,即
![]() , (1.4−1)
, (1.4−1)
并且系数![]() 被
被![]() 唯一确定。 这时
唯一确定。 这时![]() 称为用线性组合来表示共线矢量的基底。
称为用线性组合来表示共线矢量的基底。
证 如果 (1.4−1) 成立,即有![]() , 那么
, 那么![]() 与
与![]() 共线。
共线。
反过来,如果![]() 与非零矢量
与非零矢量![]() 共线,那么一定存在实数
共线,那么一定存在实数![]() ,使得
,使得![]() (见上一节中(1.3-5)的证明)。 显然如果
(见上一节中(1.3-5)的证明)。 显然如果![]() ,则
,则![]() ,即
,即![]() 。
。
最后证明 (1.4−1) 中的![]() 是唯一的。
是唯一的。
如果![]() , 那么
, 那么![]() , 而
, 而![]() , 所以
, 所以![]() .
.
定理2 如果矢量![]() 不共线,那么矢量
不共线,那么矢量![]() 与
与![]() 共面的充要条件是
共面的充要条件是![]() 可以用矢量
可以用矢量![]() 线性表示,或者说矢量
线性表示,或者说矢量![]() 可以分解成
可以分解成![]() 时的线性组合,即
时的线性组合,即
![]() , (1.4−2)
, (1.4−2)
并且系数![]() 被
被![]() 唯一确定。这时
唯一确定。这时![]() 称为用线性组合来表示共面矢量组的基底。
称为用线性组合来表示共面矢量组的基底。
证 首先,因为矢量![]() 与
与![]() 不共线,所以
不共线,所以![]() ,
,![]() 。设
。设![]() 和
和![]() 共面,如果
共面,如果![]() 和
和![]() (或
(或![]() )共线,那么根据定理1,有
)共线,那么根据定理1,有![]() , 其中
, 其中![]() (或
(或![]() ), 如果
), 如果![]() 和
和![]() 都不共线,把它们归结到共同的始点
都不共线,把它们归结到共同的始点![]() , 并设
, 并设![]() ,
,![]() ,
,
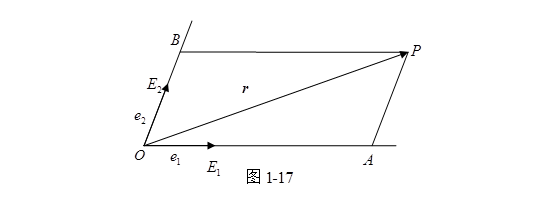
那么经过![]() 的终点
的终点![]() 分别作
分别作![]() 的平行线依次与直线
的平行线依次与直线![]() 交于
交于![]() ( 图1-17 ). 因为
( 图1-17 ). 因为![]() ,根据定理1,可设
,根据定理1,可设![]() ,
,
所以根据矢量加法的平行四边形法则得![]() , 即
, 即
![]() .
.
反过来,设![]() , 如果
, 如果![]() 有一是零,例如
有一是零,例如![]() ,
,
那么![]() 与
与![]() 共线,因此它与
共线,因此它与![]() 共面。
共面。
如果![]() , 那么
, 那么![]() , 从两矢量相加的平行四形法则可知
, 从两矢量相加的平行四形法则可知![]() 与
与![]() 与
与![]() 共面,因此
共面,因此![]() 与
与![]() 共面。
共面。
最后证明![]() 由
由![]() 唯一确定。
唯一确定。
因为如果![]() , 那么
, 那么![]() , 如果
, 如果![]() , 那么
, 那么![]() , 将有
, 将有![]() , 这与定理假设矛盾,所以
, 这与定理假设矛盾,所以![]() . 同理,
. 同理,![]() , 因此
, 因此![]() 被唯一确定。
被唯一确定。
定理3 如果矢量![]() 不共面,那么空间任意矢量
不共面,那么空间任意矢量![]() 可以由矢量
可以由矢量![]() 线性表示,或者说空间任意矢量
线性表示,或者说空间任意矢量![]() 可以分解成矢量
可以分解成矢量![]() 的线性组合,即
的线性组合,即
![]() , (1.4-3)
, (1.4-3)
并且其中系数![]() 被
被![]() 唯一确定。
唯一确定。
这时称![]() 为用线性组合来表示空间矢量的基底。
为用线性组合来表示空间矢量的基底。
证 首先因为![]() 不共面,所以
不共面,所以![]() ,且它们两两不共线。
,且它们两两不共线。
如果![]() 和
和![]() 之中两个矢量共面,那么根据定理1.4.2 立即可知(1.4-3)成立,例如
之中两个矢量共面,那么根据定理1.4.2 立即可知(1.4-3)成立,例如![]() 和
和![]() 共面,那么有
共面,那么有![]() 等等。
等等。
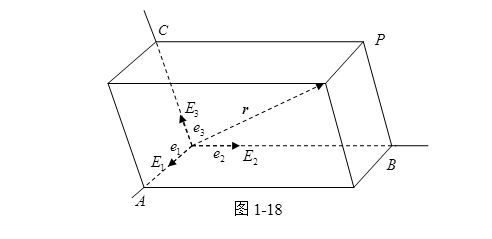
如果![]() 和
和![]() 之中任何两个矢量都不共面,将矢量
之中任何两个矢量都不共面,将矢量![]() 和
和![]() 归结到共同的始点
归结到共同的始点![]() ,并设
,并设![]() ,过
,过![]() 的终点
的终点![]() 作三平面分别与平面
作三平面分别与平面![]() 平行,且分别和直线
平行,且分别和直线![]() 相交于
相交于![]() 三点,因
三点,因
此作成了以![]() 为棱,
为棱,![]() 为对角线的平行六面体(图 1-18),于是得到:
为对角线的平行六面体(图 1-18),于是得到:
![]() ,
,
又根据定理1,可设![]() , 所以得到
, 所以得到
![]()
下面证明系数![]() 由
由![]() 唯一确定。
唯一确定。
因为如果
![]() ,
,
那么
![]()
如果
![]()
那么
![]()
根据定理2可知![]() 共面,这与定理假设矛盾,所以有
共面,这与定理假设矛盾,所以有 ![]() 。
。
同理,![]() ,因此
,因此![]() 被唯一确定。
被唯一确定。
例 1 已知三角形![]() , 其中
, 其中![]() , 而
, 而![]() 分别是三角形两边
分别是三角形两边![]() 上的点,且有
上的点,且有![]() ,
, ![]() ,设
,设![]() 与
与![]() 相交于
相交于![]() 图(1-19),试把矢量
图(1-19),试把矢量![]() 分解成
分解成![]() 的线性组合。
的线性组合。
解 因为![]() , 或
, 或![]()
而 ![]() ,
,![]() ,
,
![]()
所以 ![]() , (1)
, (1)
或 ![]() (2)
(2)
因此![]() 不共线,所以根据定理2,由(1),(2)得:
不共线,所以根据定理2,由(1),(2)得:
![]()
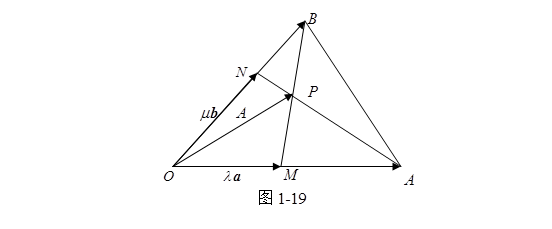
解得:
![]()
所以得:
![]() ,
,
即
![]()
例 2 证明四面体对边中点的连线交与一点,且互相平分。
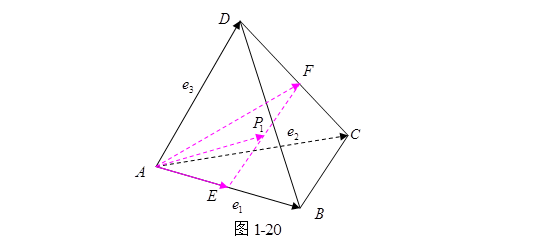
证 设四面体![]() 一组对边
一组对边![]() 的中点分别为
的中点分别为![]() ,连线为
,连线为![]() 的中点为
的中点为![]() (图1-20),其余二组对边中点连线的中点分别为
(图1-20),其余二组对边中点连线的中点分别为![]() , 下面只要证明
, 下面只要证明![]() 三点重合就可以了。 记
三点重合就可以了。 记![]() 。
。
连接![]() ,因为
,因为![]() 是
是![]() 的中线,所以
的中线,所以![]() ,
,
又因为![]() 是
是![]() 的中线,所以
的中线,所以 ![]() ,
,
而 ![]() ,
,
从而得 ![]() ,
,
同理可得 ![]()
所以 ![]() ,
,
从而知三点![]() 重合,命题得证。
重合,命题得证。
我们还可以把矢量的线性组合的概念加以扩充,引进线性相关和线性无关的概念。
定义2 对于 n(n≥1) 个矢量![]() , 如果存在不全为零的 n 个实数
, 如果存在不全为零的 n 个实数![]() 使得
使得
![]() , (1.4−4)
, (1.4−4)
那么矢量![]() 称为线性相关,否则称为线性无关。 换句话说,矢量
称为线性相关,否则称为线性无关。 换句话说,矢量![]() 称为线性无关的是指只有
称为线性无关的是指只有![]() 时, (1.4−4) 才成立。
时, (1.4−4) 才成立。
推论1 一个矢量![]() 线性相关的充要条件为
线性相关的充要条件为![]() 。
。
定理4 在 n≥2 时,矢量![]() 线性相关的充要条件是其中有一个矢量是其余矢量的线性组合。
线性相关的充要条件是其中有一个矢量是其余矢量的线性组合。
证 一方面,设![]() 线性相关,那么(1.4-4)成立,且
线性相关,那么(1.4-4)成立,且![]() 中至少有一个不等于
中至少有一个不等于![]() ,不妨设
,不妨设![]() , 那么
, 那么![]() 可以写成
可以写成![]() 的线性组合
的线性组合
![]()
反过来,不妨设![]() 中有一个矢量
中有一个矢量![]() ,它是其余矢量的线性组合,即
,它是其余矢量的线性组合,即
![]() ,
,
改写一下,就有
![]()
因为数![]() 不全为0, 所以
不全为0, 所以 ![]() 线性相关。
线性相关。
定理5 如果一组矢量中的一部分矢量线性相关,那么这一组矢量就线性相关。
证 设有一组矢量![]() , 其中一部分比如说
, 其中一部分比如说![]() 线性相关,即有不全为零的数
线性相关,即有不全为零的数![]() 使得
使得 ![]() ,
,
由上式显然有
![]() ,
,
因为![]() 中至少有一不等于0,所以
中至少有一不等于0,所以![]() 线性相关。
线性相关。
推论2 一组矢量如果含有零矢量,那么这组矢量间必线性相关。
利用矢量间的线性相关的概念,可以把矢量间的共线与共面的条件推广到更一般的形式。
定理6 两矢量共线的充要条件是它们线性相关。
证 设两矢量为![]() 与
与![]() ,如果它们线性相关,那么有
,如果它们线性相关,那么有![]() ,
,
并且![]() 不全为零,不妨设
不全为零,不妨设![]() , 从而得
, 从而得![]() 。
。
如果![]() , 据定理1知
, 据定理1知![]() 与
与![]() 共线;如果
共线;如果![]() , 显然
, 显然![]() 与
与![]() 共线。
共线。
反过来,设![]() 与
与![]() 共线,如果
共线,如果![]() , 那么据定理1知
, 那么据定理1知![]() ,
,
即 ![]() , 所以
, 所以![]() 与
与![]() 线性相关;如果
线性相关;如果![]() , 那么由推论2知,
, 那么由推论2知, ![]() 与
与![]() 线性相关。
线性相关。
这个定理告诉我们,如果要判别两矢量![]() 与
与![]() 共线,只要判别是否存在不全为零得两个数
共线,只要判别是否存在不全为零得两个数![]() ,使得
,使得
![]() . (1.4−5)
. (1.4−5)
类似地,读者自己可以证明下面的定理。
定理7 三矢量共面的充要条件是它们线性相关。
按照这个定理,要判别三个矢量![]() 是否共面,只要判别 是否存在不全为零的三个数
是否共面,只要判别 是否存在不全为零的三个数![]() , 使得
, 使得
![]() (1.4−6)
(1.4−6)
对于空间的任何四个或四个以上的矢量,我们有下面的定理与推论。
定理8 空间任何四个矢量总是线性相关。
证 设四矢量为![]() , 如果
, 如果![]() 共面,那么根据定理7 它们线性相关。再根据定理5,即知所说四个矢量线性相关;如果
共面,那么根据定理7 它们线性相关。再根据定理5,即知所说四个矢量线性相关;如果![]() 不共面,由定理3可设
不共面,由定理3可设![]() , 根据定理4知
, 根据定理4知![]() 线性相关。
线性相关。
由本定理结合定理1.4.5立即可得:
推论3 空间四个以上矢量总是线性相关。
例 3 设![]() , 试证
, 试证![]() 三点共线的充要条件是存在不全为零的实数
三点共线的充要条件是存在不全为零的实数![]() 使得
使得 ![]() , 且
, 且![]() .
.
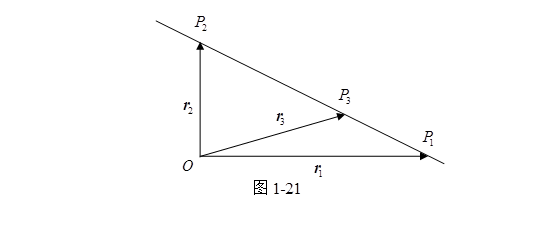
证 设![]() 三点共线,那么
三点共线,那么![]() 两矢量共线,因此两矢量
两矢量共线,因此两矢量![]() 与
与![]() 线性相关,所以存在不全为0的数
线性相关,所以存在不全为0的数![]() ,使得
,使得
![]() .
.
即
![]() ,
,
由此得
![]() ,
,
令
![]() ,
,
则![]() 不全为零,
不全为零,
且
![]() , 且
, 且![]() .
.
反过来,设有不全为0的数![]() 使
使
![]() , 且
, 且![]() .
.
根据条件不妨设![]() , 代入上面矢量等式整理得
, 代入上面矢量等式整理得
![]()
即
![]() ,
,
但由 ![]() 知
知![]() 不全为零,所以
不全为零,所以![]() 共线,
共线,
也就是![]() 三点共线。
三点共线。
例 4 设![]() 为两不共线矢量,证明矢量
为两不共线矢量,证明矢量![]() ,
,![]() 共线的充要条件是
共线的充要条件是
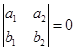 .
.
证 根据定理6,![]() 两矢量共线的充要条件是存在不全为零的数
两矢量共线的充要条件是存在不全为零的数![]() 使得
使得
![]() ,
,
即
![]() ,
,
因为![]() 为不共线的矢量,也就是两矢量
为不共线的矢量,也就是两矢量![]() 线性无关。
线性无关。
所以
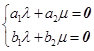 ,
,
又因为![]() 不全为零,从而得矢量
不全为零,从而得矢量![]() 与
与![]() 共线的充要条件为
共线的充要条件为
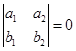 .
.
