在这里，平面上的曲线（包括直线），都是看成具有某种特征性质的点的集合。曲线上点的特征性质，包含着两方面的意思，就是：1）曲线上的点都具有这些性质；2）具有这些性质的点都在曲线上。因此曲线上点的特征性质，也可以说成是点在曲线上的充要条件。

曲线上点的特征性质，在建立了坐标系的平面上，它反映为曲线上点的两个坐标与所应满足的相互制约条件，一般用方程或来表达。

定义1  当平面上取定了坐标系之后，如果一个方程与一条曲线有着关系：

1）满足方程的必是曲线上某一点的坐标：

2）曲线上任何一点的坐标满足这个方程，

那么这个方程就叫做这条曲线的方程，而这条曲线叫做这个方程的图形。

为了方便起见，“点的坐标满足方程”这句话常说成“点满足方程”。

根据曲线方程的定义，曲线上的点与其方程的解之间有着一一对应关系。这样研究曲线的几何问题，就可以转化为研究其方程的代数问题了。

求一条曲线的方程实际上就是将这条曲线上的点的特征性质，用关于曲线上的点的两个坐标的方程来表达。

例1 求圆心在原点，半径为的圆的方程。

解  根据圆的定义，圆上任意点的特征性质，即在圆上的充要条件是到圆心的距离等于半径，即

(1)

应用两点距离公式得

(2.1-1)

两边平方得

由于方程(2.1-1)与(1)同解，所以(2.1-1)即为所求圆的方程。

完全类似地，可以求得圆心在半径为的圆的方程是

(2.1-2)

求曲线的方程，有时在化简过程中，会增添不属于给定条件的内容，这时，必须从方程开始检查一下，把方程中代表那些不符合给定条件的点去掉。

例2  已知两点和，求满足条件的动点的轨迹方程。

解  动点在轨迹上的充要条件是

用点的坐标来表达就是

(2)

移项得

两边平方整理得

(3)

再两边平方整理得

(4)

因为方程（2）与（3）同解，而方程（4）与（3）却不同解，但当方程（4）附加了条件后，方程（4）与（3）同解，从而方程（4）与（2）同解，所以方程

为所求动点的轨迹方程。

这里在方程中附加了条件，其意思就是在方程中除去使的解，因为这些是不符合给定条件的多余的部分。所求的轨迹是反比函数的图象——双曲线的一支，即第一象限中的部分（图2-1中实线部分）。

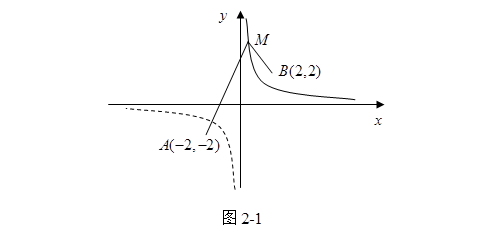
在解析几何中，曲线又常常表现为一个动点运动的轨迹，但是运动的规律往往不是直接反映为动点的两个坐标与之间的关系，而是直接表现为动点的位置随着时间改变的规律。当动点按照某种规律运动时，与它对应的矢径也将随时间的不同而改变（模与方向的改变），这样的矢径，我们称它为变矢，记做。如果变数的每一个值对应于变矢的一个完全确定的值（模与方向），那么我们就说是变数的矢性函数，并把它记做

(2.1-3)

显然当变化时，矢量的模与方向一般也都随着改变。

设平面上取定的标架为，矢量就可用它的分量来表达，这样矢性函数(2.1-3)就可以写为

(2.1-4)

其中是的分量，它们分别是变数的函数。

定义2  若取的一切可能取的值，由(2.1-4)表示的矢径的终点总在一条曲线上；反过来，在这条曲线上的任意点，总对应着以它为终点的矢径，而这矢径可由的某一值通过(2.1-4)完全决定，那么就把表达式(2.1-4)叫做曲线的矢量式参数方程，其中的为参数。

换句话说，(2.1-4)叫做一条曲线的矢量式参数方程，如果当在区间内变动时，矢径的终点就描绘出这条曲线来（图2-2）。

因为曲线上点的矢径的分量为，所以曲线的参数方程常写成下列形式

        

(2.1-5)

我们把表达式(2.1-5)叫做曲线的坐标式参数方程。

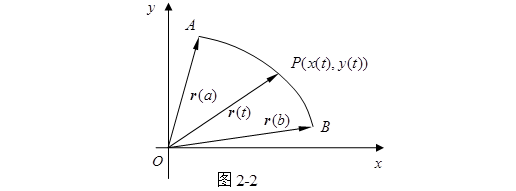
如果从(2.1-5)中消去参数（如果可能的话），那么就能得出曲线的普通方程

例3  已知直线通过定点，并且它与非零矢量共线，求直线的方程。

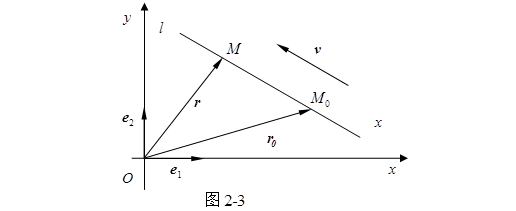
解  设为直线上的任意点，并设（图2-3），那么点在上的充要条件为矢量与共线，也就是

                        

这里的是随着点而定的实数。又因为

所以

即

(2.1-6)

这就是直线的矢量式参数方程，式中的为参数。

由(2.1-6)容易得到直线的坐标式参数方程为

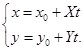
(2.1-7)

直线的参数方程中的参数，有一个简单的几何意义，就是当是单位矢量时，那么点与之间的距离就等于，这是因为

与直线共线的非零矢量叫做直线的方向矢量，显然，任何一个与直线共线的非零矢量，都可以作为直线的方向矢量。

由直线的参数方程(2.1-7)消去参数得

(2.1-8)

方程(2.1-8)叫做直线的对称式方程或标准式方程，它是一个二元一次方程，可以把它写成

 

(2.1-9)

这里。

反过来，任意一个二元一次方程(2.1-9)都表示直线，这是因为它总能化成(2.1-8)的形式。事实上，在方程(2.1-9)中任取一组解，那么有

所以(2.1-9)可以改写成

或

方程(2.1-9)叫做直线的一般方程。从上面我们看到直线一般方程(2.1-9)中系数与的几何意义是：矢量是直线(2.1-9)的一个方向矢量，在直角坐标系下，显然有垂直于矢量，从而垂直于直线(2.1-9)，我们称为直线(2.1-9)的法矢量。

给定两直线

那么与的方向矢量分别为，由两直线的方向矢量读者容易知道：

两直线与相交的充要条件为

(2.1-10)

两直线与平行的充要条件为

 

(2.1-11)

两直线与重合的充要条件为

 

(2.1-12)

而在直角坐标系下，两直线与的交角为

(2.1-13)

从而有

(2.1-14)

例4  一个圆在一直线上无滑动地滚动，求圆周上的一点的轨迹。

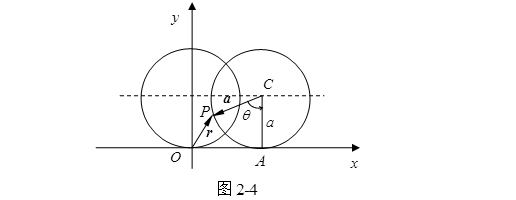
解  取直角坐标系，设半径为的圆在轴上滚动，开始时点恰好在原点（图2-4），经过一段时间的滚动，圆与直线的切点移到点，圆心移到的位置，这时有

设，于是矢量对轴所成的有向角为

, 

则

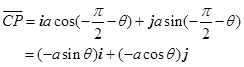
又 

所以

(2.1-15)

(2.1-15)是点轨迹的矢量式参数方程，其中为参数。设点的坐标为，那么由(2.1-15)式容易得点的坐标式参数方程为

(2.1-16)

取时，消去参数，便得到点轨迹在时的一段的普通方程

(2.1-17)

这个方程要比参数方程(2.1-16)复杂得多。

当圆在直线上每转动一周时，点在一周前后的运动情况总是相同的，因此曲线是由一系列完全相同的拱形曲线组成(图2-5)，这种曲线叫做旋轮线或称为摆线。

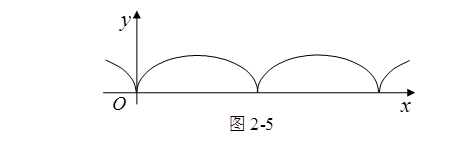
例5  已知大圆半径为，小圆半径为，设大圆不动，而小圆在大圆内无滑动地滚动，动圆周上某一定点的轨迹叫做内旋轮线（或称内摆线），求内旋轮线的方程。

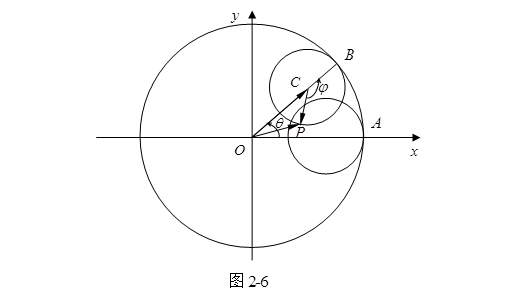
解  设运动开始时动点与大圆周上的点重合，并取大圆中心为原点，为轴，过点垂直于的直线为轴（图2-6），经过某一过程后，小圆与大圆的接触点为，并设小圆中心为，那么一定在半径上，显然有

设

那么

且有

所以

矢量对轴所成的有向角为

由于，所以

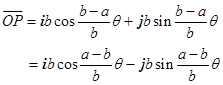
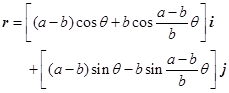
(2.1-18)

此式就是内旋轮线的矢量式参数方程，式中为参数。设P点的坐标为，那么由（2.1-18）式容易得内旋轮线的坐标式参数方程为

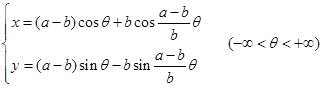
(2.1-19)

特殊地，当时，应用公式

曲线方程(2.1-19)便化为

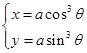
(2.1-20)

这条曲线叫做四尖点星形线（图2-7）。

 

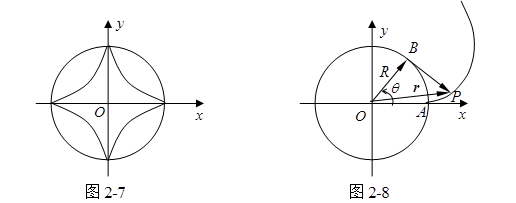
例 6  把线绕在一个固定圆周上，将线头拉紧后向反方向旋转，以把线从圆周上解放出来，使放出来的部分成为圆的切线，求线头的轨迹。

解  设圆的半径为，线头的最初位置是圆周上的点，以圆心为原点，为轴，经过一过程后，切点移至，为切线（如图2-8），那么

设，那么

且矢量对轴所成的有向角为

而

所以

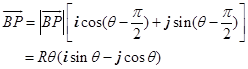
所以

（2.1-21）

(2.1-21)就是所求点轨迹的矢量式参数方程，其中为参数。如果设的坐标为，那么由(2.1-21)得该轨迹的坐标式参数方程为

(2.1-22)

由（2.1-21）或(2.1-22)表示的曲线，叫做圆的渐伸线或称切展线，这种曲线在工业上常被采用为齿廓曲线。

曲线的参数方程，是解析几何联系实际的一个重要的工具，有的时候运用参数方程来表达曲线，要比普通方程简单得多，甚至有的曲线只能用参数方程表示，即不能用的初等函数来表示，例如参数方程

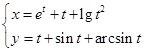
便是这样的例子。

消去曲线参数方程中的参数就得到曲线的普通方程，反过来，我们也可以把曲线的普通方程改写为参数方程的形式，一般地适当选取参数，找出变数与参数的关系式，然后代入原方程求出，那么就是曲线的参数方程。在这里当然也可先找出与的关系式，然后代入原方程求出，从而得曲线的参数方程。

例7  把椭圆的普通方程改写为参数方程。

解  设，代入原方程得

 

如果取，令，那么

可以变形为

所以取为参数，且, 那么椭圆的参数方程式为

在化曲线的普通方程为参数方程时，由于选取的参数不是唯一的，所以关系式可以有不同的形式，从而同一条曲线的参数方程也可以有多种表达形式。例如在例7中，如果设

代入原方程得

由此解得

在第二式中取，得，所以舍去第一式，取

从而得          

如果令，那么有

,  

所以椭圆的参数方程另一种表达形式为

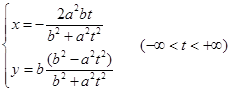
在第二种解法中，我们设，它实际上是在椭圆上取定上点，作以点为中心的直线束，而这时的椭圆的参数方程恰为直线束中的直线与椭圆交点的坐标的一般表达式。由于这时过点的轴的斜率不存在，因此尚需补上点，或者把它看成当时的交点。

仿此，在化方程

为参数方程时，我们只要设，就能求得它的参数方程为

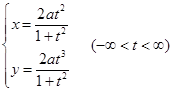
在曲线的参数方程与普通方程互化时，必须注意两种不同形式的方程应该等价，因为它们是代表同一条曲线。但是在互化时往往由于变数的允许值可能产生变化，因而可能导致两者所表示的曲线不完全一样，例如化方程为参数方程时，如果令，那么参数方程为

因为，所以有，因此，这时参数方程所表示的曲线只是原曲线的一部分，两方程不等价。但如果令，代入原方程得

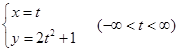
这参数方程所表示的曲线与原曲线一致，所以它与原方程等价，也就是说它是原曲线的参数方程。

再如参数方程，由于，所以表示的曲线只是第一象限里的部分，而消去参数后得普通方程为，它表示整条抛物线，与原曲线比较增添了第四象限里的部分。但是如果附加了条件，那么两方程就等价了，因此它的普通方程就写成。