1 曲面的方程

空间曲面方程的意义和平面曲线的方程是一相样的，那就是在空间建立坐标系之后，把曲面（作为点轨迹）上的点的特征性质，用点的坐标与之间的关系式来表达，一般是用方程

                      （1）

或

                        （1’）

来表达；反过来，每一个形如（1）或（1’）的方程通常表示空间的一个曲面，例如在空间取定一个坐标系后，满足(1’)的任意一组解就确定一个点，而当连续变动时，点就画出一个图形来（图2-9），这就是(1’)的图形，一般是一个曲面。

定义1  如果一个方程(1)或(1’)与一个曲面有着关系：1）满足方程(1)或(1’)的是曲面上的点的坐标：2）曲面上的任何一点的坐标满足方程(1)或(1’)，那么方程(1)或(1’)就叫做曲面的方程，而曲面叫做方程(1)或(1’)的图形。

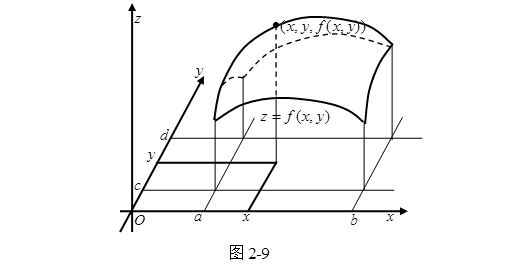
曲面的方程有时没有实点满足它，这时方程不表示任何实图形，我们称它为虚曲面，如；有时只有一个实点满足它，例如方程，只有点满足它，因此它只表示坐标原点；也有时代表一条曲线，例如方程，只有当的点能满足它，因此它表示轴，是一条直线。

下面我们举例说明怎样从曲面（作为点的轨迹）上点的特征性质来导出曲面的方程。

例1  求连结两点和的线段的垂直平分面的方程。

解  垂直平分面可以看成到两定点和为等距离的动点的轨迹，因此垂直平分面上的点的特征性质为

                        

而              

从而得           

             

化简得

即为所求的垂直平分面的方程。

例2  求两坐标面和所成二面角的平分面方程。

解  因为所求的平分面是与两坐标平面和有等距离的点的轨迹，因此点在平分面上的充要条件是

                             

所以                          

或写成                         

因此所求的角平分面的方程是

    与    

例3  求坐标平面的方程

解  很明显，这平面是坐标为零的点的轨迹。因此它的方程是。

同样，坐标平面与的方程分别是与。

例4  一平面平行于坐标平面，且在轴的正向一侧与平面相隔距离为，求它的方程。

解  所求的平面上各点的坐标都等于，所以平面方程为。

例5  设球面的中心是点，而且半径等于，求它的方程。

解  设是球面上的任意点，那么根据球的定义，球面上的点的特征性质是 

而            

得所求的球面方程

                   (2.2-1)

特别地，以原点为球心的球心的球面方程是

                          (2.2-2)

将（2.2-1）展开后得

因此球面方程是一个三元二次方程，它的所有平方项的系数相等，交叉项消失。

反过来，如果三元二次方程

当时，方程可化为

            (2.2-3)

的形式，配方得

如果，那么(2.2-3)表示实的球面。

如果，那么(2.2-3)表示空间一点。

如果，那么(2.2-3)表示无实图形。

习惯上，我们把上面的点叫做点球，无实图形时叫做虚球面，这三种情形统称为球面。因此球面的方程是一个平方项系数相等而交叉项消失的三元二次方程；反过来，任何一个三元二次方程，如果它的二次需系数相等，而且交叉项消失，那么它一定表示一个球面（实球面，点或虚球面）。

2  曲面的参数方程

我们知道，平面曲线的参数方程，是以单参数的矢函数

或

定义的，空间曲面的参数方程与平面曲线的参数方程非常类似。设在两个变数的变动区域内定义了双参数矢函数

                     (2.2-4)

或

         (2.2-5)

这里是变矢的分量，它们都是变数的函数。当取遍变动区域的一切值时，径矢

的终点所画成的轨迹，一般为一张曲面（图2-10）。

定义2  如果取的一切可能取的值，由(2.2-5)表示的径矢的终点总在一个曲面上；反过来，在这个曲面上的任意点总对应着以它为终点的径矢，而这径矢可由的值通过(2.2-5)完全决定，那么我们就把表达式(2.2-5)叫做曲面的矢量式参数方程，其中为参数。

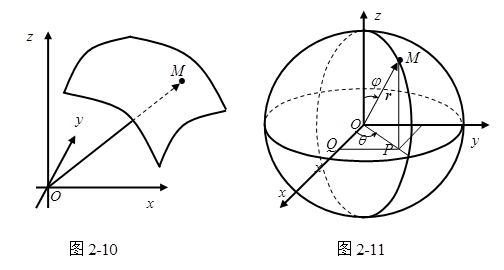
 因为径矢的分量为,所以曲面的参数方程也写为

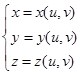                     (2.2-6)

表达式(2.2-6)叫做曲面的坐标式参数方程。

例6  求中心在原点，半径为的球面的参数方程。

解  设是以坐标原点为中心，为半径的球面上的任一点，在坐标面上的射影为，而在轴上的射影为。又设在坐标面上的有向角，轴与的交角（图2-11），那么

且                 

所以

       (2.2-7)

这就是中心在原点，半径为的球面的矢量式参数方程。它的坐标式参数方程为

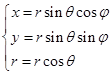                     (2.2-8)

(2.2-7)或(2.2-8)中的与为参数，它们的取值范围分别是与。

例7  求以轴为对称轴，半径为的圆柱面的参数方程

解  设圆柱面上的任意一点，在坐标面上的射影为(图2-12)。再设面上的有向角，在轴上的射影为，那么

而

所以

              (2.2-9)

这就是圆柱面的矢量式参数方程，它的坐标式参数方程为

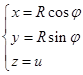                       (2.2-10)

(2.2-9)或(2.2-10)中的与为参数，它们的取值范围分别是。

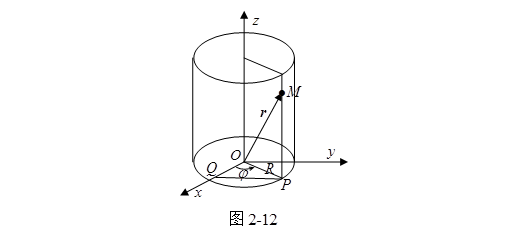
空间曲面的参数方程与平面上的曲线的参数方程一样，它的表达形式也不是唯一的。比如例1中，如果把参数改为由到的有向角，那么球面的参数方程为

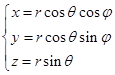
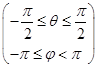         (2.2-11)