1．椭圆抛物面

定义1  在直角坐标系下，由方程

                                    (4.6-1)

所表示的曲面叫做椭圆抛物面，方程(4.6-1)叫做椭圆抛物面的标准方程，其中是任意的正常数。

显然椭圆抛物面(4.6-1)关于坐标面与对称，也关于轴对称，但是它没有对称中心，它与对称轴交于点，这点叫做椭圆抛物面(4.6-1)的顶点。

从方程(4.6-1)知

 

所以曲面全部在坐标面面的 的一侧。

用坐标面及截割曲面(4.6-1)，分别得抛物线

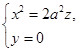                       (1)

与

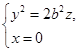                       (2)

这两个抛物线叫做椭圆抛物面(4.6-1)的主抛物线。它们有着共同的轴与相同的开口方向，即开口方向都与轴的正向一致。

用坐标平面来截曲面(4.6-1)只得一点，但用平行于面的平面来截曲面(4.6-1)，截线总是椭圆

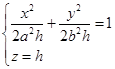                     (3)

这个椭圆的两对顶点分别为,，经们分别在抛物面(4.6-1)的主抛物线（1）与（2）上（图4-15）。因引，椭圆抛物面(4.6-1)可以看成是由一个椭圆的变动（大小位置都改变）而产生的。这个椭圆在变动中，保持所在平面平行于平面，且两对顶点分别在抛物线（1）与（2）上滑动。

图4-15是椭圆抛物面(4.6-1)的图形。

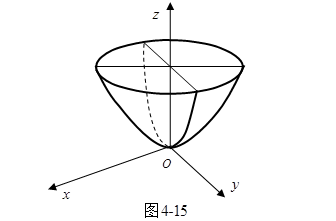
如果我们用平行于面的平面截割椭圆抛物面(4.6-1)得抛物线

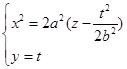                       (4)

显然抛物线（4）与主抛物线（1）全等，且它所在的平面平行于主抛物线（1）所在的平面并且与（1）有相同的开口方向。此外，抛物线（4）的顶点位于主抛物线（2）上，因此我们得到下面的结论：

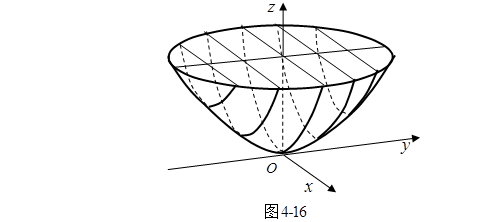
如果取两个这样的抛物线，它们所在的平面互相垂直，它们的顶点和轴都重合，而且两抛物线有相同的开口方向，让其中一条抛物线平行于自己（即与抛物线所在的平面平行），且使其顶点在另一个抛物线上滑动，那么这一抛物线的运动轨迹便是一个椭圆抛物面（图4-16）。

在方程(4.6-1)中，如果，那么方程变为（4.3-5），即

                  

这时截线（3）为一圆，曲面就成为旋转抛物面。

2．双曲抛物面

定义2  在直角坐标系下，由方程

                             (4.6-2)

所表示的曲面叫做双曲抛物面，方程(4.6-2)叫做双曲抛物面的标准方程，其中为任意的正常数。

显然曲面(4.6-2)关于面，面与轴对称，但是它没有对称中心。

用坐标面去截割曲面(4.6-2)，就得

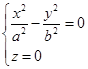                             (5)

这是一对相交于原点的直线

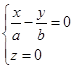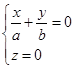  与                       （5'）

其次用坐标平面与来截割曲面(4.6-2)，分别得两抛物线

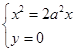                             (6)

与

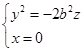                            (7)

这两抛物线叫做双曲面的主抛物线，它们所在的平面相互垂直，有相同的顶点与对称轴，但两抛物线的开口方向不同，抛物线（6）沿轴正向开口，而抛物线（7）沿轴负向开口。

如果用平行于面的平面来截曲面(4.6-2)，截线总是双曲线

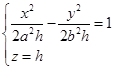                          (8)

当时，双曲线（8）的实轴与轴平行，虚轴与轴平行，顶点在主抛物线（6）上；当时，双曲线（8）的实轴与轴平行，虚轴与轴平行，顶点在主抛物线（7）上（图4-17）。

因此，曲面(4.6-2)被平面分割成上下两部分，上半部沿轴的两个方向上升，下半部沿轴的两个方向下降，曲面的大体形状象一只马鞍子，所以双曲抛物面也叫做马鞍面（图4-17）。

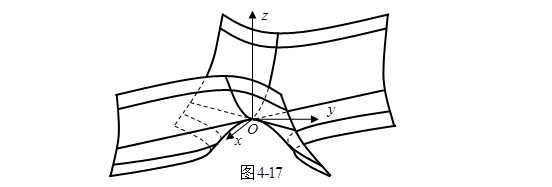
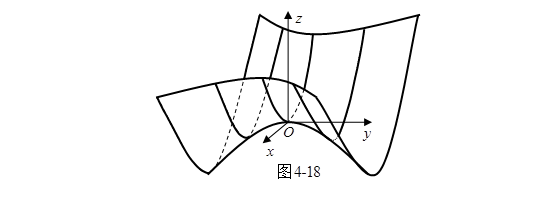
双曲抛物面的形状比较复杂，为了进一步明确它的结构，我们再来观察用平行于面的一组平行平面来截割曲面(4.6-2)所得的截线，这时截线为抛物线

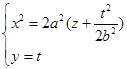                     (9)

我们容易看出，不论取怎样的实数，所截得的抛物线（9）总与主抛物线（6）是全等的，且所在平面平行于这个主抛物线所在的平面，而它的顶点则在另一抛物线（7）上（图4-18），于是得到下面的结论：

如果取两个这样的抛物线，它们的所在平面互相垂直，有公共的顶点与轴，而两抛物线的开口方向相反，让其中的一个抛物线平行于自己（即与抛物线所在的平面平行），且使其顶点在另一抛物线上滑动，那么这一抛物线的运动轨迹便是一个双曲抛物面。

椭圆抛物面与双曲抛物面统称为抛物面，它们都没有对称中心，所以又叫做无心二次曲面。

例1  作出球面与旋转抛物面的交线。

解  两曲面的交线为

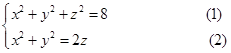
（2）代入（1）得

                  

即                

所以               或 

由（2）知，所以取，因此交线方程可改写为

                    

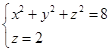
或

                 

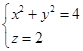
这是平面上的一个圆，圆心为，半径为，它的图形如图4-19所示。

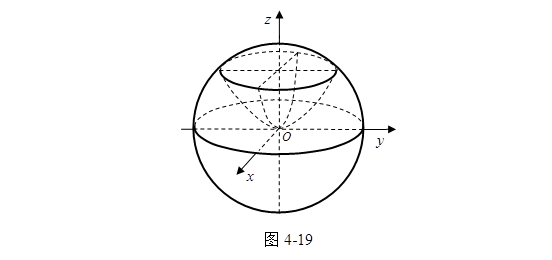
例2  作出曲面与平面，三坐标面所围成的立体在第一卦限部分的立体图形。

解  为抛物柱面，它的母线平行于轴，准线为面上的抛物线，抛物线的顶点为，焦参数，开口方向与轴的方向相反。

平面平行于轴，它与面的交线是一条直线，这条直线与轴，轴分别交于点，。

为了画出这张立体图，还必须画出已知抛物柱面与平面的交线，为此我们设想用一平行于的平面来截割它们，那么截得一矩形（图4-20），其中为抛物柱面的母线，为交线上的点，这样我们就得到下面描绘交线上的任意点的方法：在抛物线弧上任取一点，过作抛物柱面的母线，再作轴，交轴于，过作轴，交于，再过作直线，交于点，那么即为交线上的点。用此方法可得交线上一系列的点，把这些点连结起来，即得所求抛物柱面与平面的交线。所求立体图如图4-20所示。