一、多元线性回归方程

多元线性回归方程是表达一个因变量与2个或2个以上的自变量之间的线性依存关系的一种多元线性回归模型的估计式。

多元线性回归模型的一般表达式为：

上式中，b0表示截距，bi分别表示与个自变量想联系的斜率(或称为偏回归系数)，ui表示剩余残差项或称为随机扰动项，假定。

多元线性回归方程为：      

上式中，表示多元线性回归模型的估计式，当回归系数都确定后，代如各自变量的值后得到的是多元线性回归模型的估计值。式中bi的含义与式(8.1)中的相同。各自变量xij的下标、、……、，其中1，2，……代表第个自变量，代表某个自变量的样本数据的顺序号，=1，2，……，n。对自变量下标的解释同样适用式(8-1)。式(8.2)中的参数可由最小平方法导出的正规方程组解出，即(为简便起见，数据的顺序号省略)：

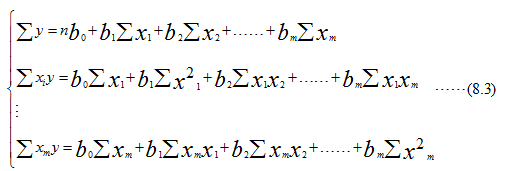
当自变量超过三个时，一般要用矩阵形式通过计算机调用多元回归分析的软件包来求出回归参数。下面以二元线性回归模型和相应的估计式——二元线性回归方程作为多元线性回归分析的特例来加以介绍。

二个自变量分别与一个因变量Y之间呈线性相关时，可用二元线性回归模型来表示：

上式中，ui表示剩余残差项或称为随机扰动项，。

上式的估计式，即二元线性回归方程为：

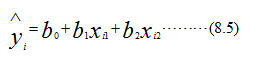
在上式中，ui表示二元线性回归的估计值；与式(8.4)中的b0相同，b0表示Y平面的截距，即当两个x都为0时Y的均值；b1和b2的解释与式(8-4)中的也相同。b1表示x2保持不变，x1增加一个单位时的平均变动量；b2表示x1保持不变x2增加一个单位时Y的平均变动量；故b1和b2分别表示与自变量x1和x2相联系的斜率，又称之0为偏回归系数。

为确定b0、b1、b2设：

通过解这个正规方程组得到二元线性回归方程中的b0、b1和b2。

二、多元线性回归方程的效果检验

(一)回归方程的显著性检验

用以判定回归的效果是否显著，即所拟和的回归方程用来解释因变量的变动是否有效，常用的方法之一是作F检验。多元线性回归方程效果检验的具体步骤为：

4.查F检验临界值表判别显著性

根据给定的已知条件之一，即显著水平，查F检验临界值表得到临界值。若检验统计量F>Fa，则认为回归效果显著；若检验统计量F<Fa,则认为回归效果不显著。

(二)回归系数的显著性检验

用以检验回归方程中的参数(或系数)作用是否显著，可用t检验法。

在多元回归分析中，如果某个自变量xi对因变量y的作用不显著，则这个自变量前的回归系数bj就可视为0。但需要指出的是：回归系数与0的差异是否大，不能根据回归系数的绝对值大小来判断，而要根据统计假设检验的理论为依据。在前面作一元回归时，对回归方程做检验时，没有介绍回归系数的t 检验。这是因为在一元回归分析中，相关系数检验、方差分析中的F检验和回归系数的t检验是具有同等作用的。只要检验其中之一就可以达到对回归方程的显著性检验的目的。但是在多元回归分析中，对多元回归方程中各个自变量相联系的回归系数应逐一进行统计检验，不能用前述的两种检验来取代。

对回归系数作t检验的步骤可归纳为：

1.计算回归估计标准误差Syx

在多元线性回归分析中，回归估计标准误差Syx的计算公式为：

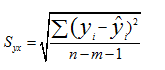
上式的根式中的分子项是实际值与估计值之差的平方和，即称之为剩余离差平方和SE；其分母项是自由度，即样本数据数减去自变量个数m后再减1，此式中的自由度计算方法和一元线性回归分析中的Syx相一致，在一元线性回归中，自变量个数m=1，则自由度为(n-1-1)=n-2。

4.查表检验显著性。

按显著性水平查自由度为n-m-1的t检验临界值表(双侧)得到临界值

若检验统计量

>，认为回归系数与0有显著差异，相应的自变量就保留在多元回归方程中；若

<

就认为该回归系数与0无显著差异，此时与相应的自变量就从多元回归方程中剔除，使建立的多元回归方程更符合实际情况。在一些情况下，如果在建立一个多元线性回归方程的过程中，同时有几个回归系数不能通过t检验，一般应剔除其中检验统计量t值最小所对应自变量后，重新建立更加简单的回归方程，然后再逐个进行回归系数的检验，反复进行到所有的回归系数都与0有显著差异时为止。