当前位置:课程学习>>第十章 抽样与参数估计>>学习内容>>知识点三
知识点三:总体参数的区间估计
○ 教师解析
一、总体均值的区间估计
根据样本平均数的分布特征可知:
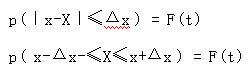
即:在概率保证程度为F(t),概率度为t的情况下,总体平均数的数值将在x-Δx和x+Δx的范围内。其中,x-Δx称为估计下限,x+Δx称为估计上限。区间[x-Δx,x+Δx]称为置信区间即由样本统计量所构造的总体参数的估计区间,估计可靠性程度称为置信度。如果我们将构造置信区间的步骤重复多次,置信区间中包含总体参数真值的次数所占的比率称为置信水平。
当总体服从正态分布且方差已知时,或者总体不是正态分布且方差未知但大样本,在这种情况下,样本均值的抽样分布均为正态分布,其数学期望是μ,方差是σ2/n,根据正态分布的性质可以得出总体均值μ所在的区间为:

如果总体服从正态分布,则不论样本容量如何,样本均值![]() 的抽样分布都服从正态分布。总体方差已知,即使在小样本的情况下也可以用(10.1)计算总体均值的置信区间。但如果总体方差未知,则需要用样本方差代替
的抽样分布都服从正态分布。总体方差已知,即使在小样本的情况下也可以用(10.1)计算总体均值的置信区间。但如果总体方差未知,则需要用样本方差代替![]() ,这是应采用t分布来建立总体均值μ置信区间。此时,总体均值的置信区间为
,这是应采用t分布来建立总体均值μ置信区间。此时,总体均值的置信区间为
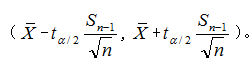
二、总体成数的估计区间
总体成数的区间估计原理与总体平均数相同,即:
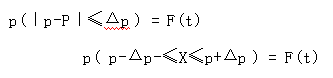
即:在概率保证程度为F(t),概率度为t的情况下,总体成数的数值将在p-Δp和p+Δp的范围内。其中p-Δp称为估计下限,p+Δp称为估计上限。区间[p-Δp,p+Δp]称为置信区间,估计可靠性程度1-α称为置信度。
当样本容量很大时,样本比例p的抽样分布可用正态分布近似。P的数学期望等于总体的比例P,而p的方差在重复抽样条件下为
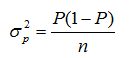
与总体均值的区间估计类似,样本比例p的基础上加减边际误差即得总体比例P的置信区间:

○ 边学边练
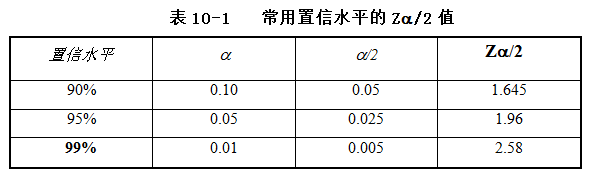
某大学从该校学生中随机抽取100人,调查他们平均每天参加体育锻炼的时间为26分钟。试以95%的置信水平估计该大学全体学生平均每天参加体育锻炼的时间(已知总体方差为36)

