当前位置:课程学习>>第四章 栅格数据模型>>电子教案>>知识点六
知识点六:栅格数据的压缩和编码
6.1 直接栅格编码
将栅格数据看做一个数据矩阵, 逐行(或逐列)记录代码,可以每行都从左到右记录,也可以奇数行从左到右、偶数行从右到左记录。如图4-11所示的栅格数据可存储记录为:AAAAABBBAABBAABB。

图4-11 直接栅格编码示例
这种记录栅格数据的文件常称为栅格文件,且常在文件头中存有该栅格数据的长宽,即行数和列数以及两方向的密度。这样,具体的像元值就可连续存储了。其特点是处理方便,但没有压缩。
6.2 栅格压缩编码
分辨率的提高和数据量之间呈平方指数关系。如果精度越大、分辨率大,数据量就越大。为了减少数据量,产生了多种压缩存储量的数据结构。通过某种编码的方法,达到减少数据长度的目的。
一、链式编码(chain codes)
链式编码又称为弗里曼链码(Freeman)或边界链码。该编码方法将数据表示为由某一原点开始并按某些基本方向确定的单位矢量链。
基本方向可定义为:东=0,东南=1,南=2,西南=3,西=4,西北=5,北=6,东北=7 等八个基本方向(图4-12)。
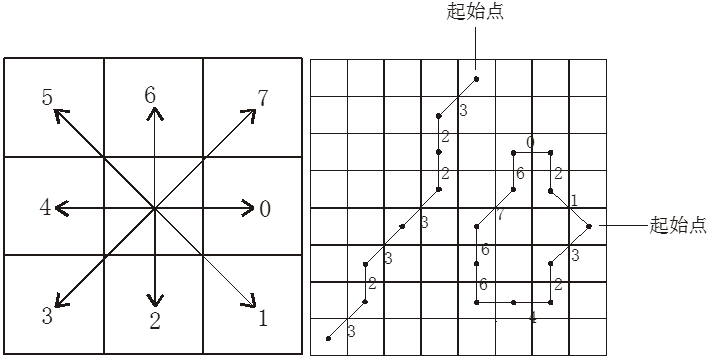
图4-12 链式编码示意图
链式编码优缺点:
优点:链式编码对多边形的表示具有很强的数据压缩能力,且具有一定的运算功能,如面积和周长计算等。探测边界急弯和凹进部分等都比较容易,比较适于存储图形数据。尤其对于线状和多边形较大区域具有较高的压缩率。
缺点:对叠置运算如组合、相交等则很难实施;对局部修改将改变整体结构,效率较低;而且由于链码以每个区域为单位存储边界,相邻区域的公共边界被重复存储会产生冗余。
二、游程长度编码(Run-Length Encoding)
也称为行程编码,其基本思想是:按行扫描,将相邻等值的像元合并,并记录代码的重复个数。将每行中具有相同属性值的连续像元映射为一个游程,每个游程的数据结构为(A,P),A表示属性值,P代表该游程最右端的列号或个数。如图4-13编码所示。
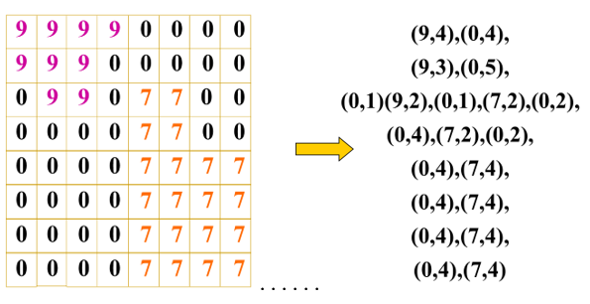
图4-13 游程编码示意图
