当前位置:课程学习>>第四章 栅格数据模型>>电子教案>>知识点七
知识点七:栅格数据的压缩和编码
7.1 矢量—栅格转换
由于矢量数据的点到栅格数据的点只是简单的坐标变换,所以,这里主要介绍线和面(多边形)的矢量数据向栅格数据的转换。
一、 线的栅格化方法
线是由多个直线段组成的,因此,线的栅格化的核心就是直线段如何由矢量数据转换为栅格数据。
设直线段的两端点坐标转换到栅格数据的坐标系后为(xA,yA)、(xB,yB),则栅格化的两种常用方法为DDA法(数字微分分析法)和Bresenham法。
(1)DDA法
如图4-15所示,设(xA,yA)、(xB,yB)与栅格网的交点为(xi,yi),则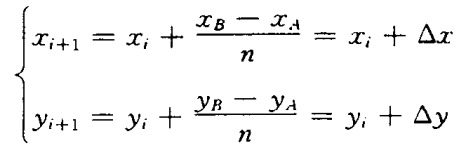
其中,
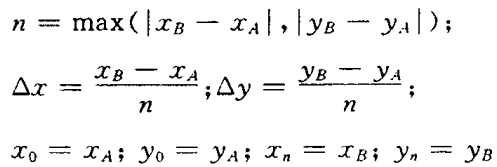
这样从i=0计算到i=n-1,即可得直线与格网的n个交点坐标,对其取整就是该点的栅格数据了。
该方法的基本依据是直线的微分方程,即dy/dx=常数。其本质是用数值方法解微分方程,通过同时对x和y各增加一个小增量来计算下一步的x,y值,即这是一种增量算法。
在该算法中,必须以浮点数表示坐标,且每次都要舍入取整。因此,尽管算法正确,但速度不够快。
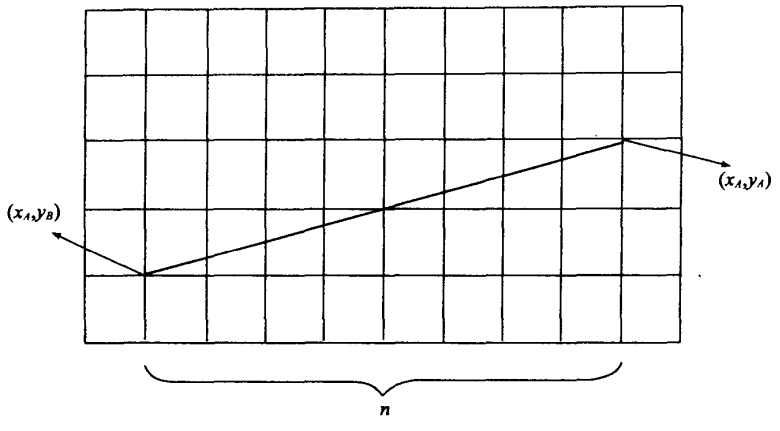
图4-15 线段变栅格示意
(2)Bresenham算法
该算法原来是为绘图机设计的,但同样适合于栅格化。该算法构思巧妙,只需根据由直线斜率构成的误差项的符号,就可确定下一列坐标的递增值。
根据直线的斜率,把直线分为8个挂限(图4-16)。例如斜率在第一挂限,范围为0.5~1,则下一点取(1,1);若斜率取0~0.5,则下一点取(1,0)。Bresenham算法不仅速度快、效果好,而且可以理论上证明它是目前同类的各种算法中最优的。
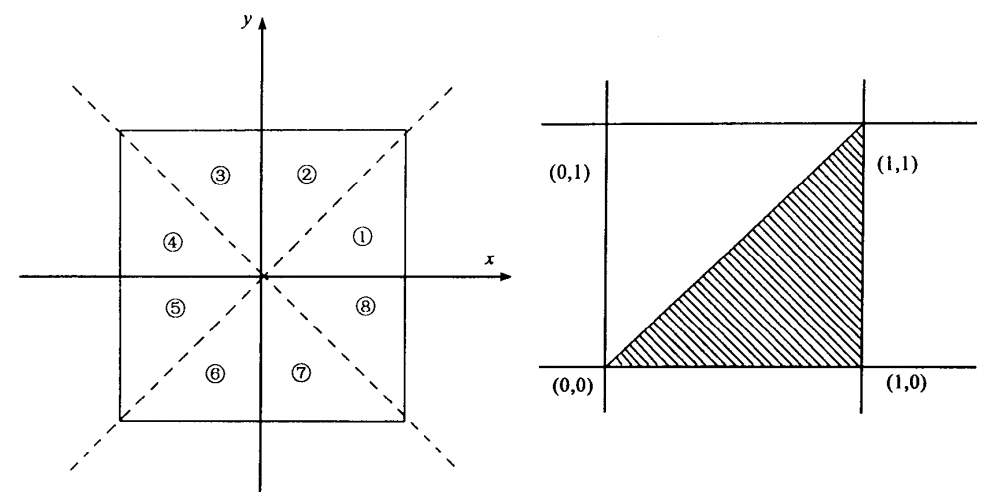
图4-16 Bresenham算法分区示意
二、 面(多边形)的栅格化方法
(1)内部点扩散法
由一个内部的种子点,向其4个方向的邻点扩散,判断新加入的点是否在多边形边界上。如果是,不作为种子点;否则当做新的种子点。直到区域填满,无种子点为止。
该算法比较复杂,而且可能造成阻塞而使扩散不能完成(如图4-17),此外,当多边形不完全闭合时,会扩散出去。
(2)扫描法
如图4-18,按扫描线的顺序,计算多边形与扫描线的相交区间,再用相应的属性值填充这些区间,即完成了多边形的栅格化。这种算法的缺点是计算量较大。
(3)边填充算法
其基本思想是:对于每一条扫描线和每条多边形边上的交点,将该扫描线上交点右方的所有像素取原属性值之补。对多边形的每条边作此处理,多边形的方向任意。
本算法的优点是算法简单,缺点是对于复杂图形,每一像素可能被访问多次,增加了运算量。为了减少边填充算法访问像素的次数,可引入栅栏。
所谓栅栏指的是一条与扫描线垂直的直线, 栅栏位置通常取多边形的顶点,且把多边形分为左右两半。栅栏填充算法的基本思路是:对于每个扫描线与多边形的交点,将交点与栅栏之间的像素用多边形的属性值取补。若交点位于栅栏左边,则将交点右边,栅栏左边的所有像素取补;若交点位于栅栏的右边,则将栅栏右边, 交点左边的像素取补。图4-19是该算法的示意图。
