当前位置:课程学习>>第八章 空间分析>>电子教案>>知识点四
知识点四:政策客体
1. 空间插值的概念和理论
空间插值常用于将离散点的测量数据转换为连续的曲面数据,以便与其它空间现象的分布模式进行比较,它包括了空间内插和外推两种算法。空间内插算法是一种通过已知点的数据推求同一区域其它未知点数据的计算方法;空间外推算法则是通过已知区域的数据,推求其它区域数据的方法。在以下几种情况下必须做空间插值:
1)现有的离散曲面的分辨率,象元大小或方向与所要求的不符,需要重新插值。例如将一个扫描影像(航空像片、遥感影像)从一种分辨率或方向转换到另一种分辨率或方向的影像。
2)现有的连续曲面的数据模型与所需的数据模型不符,需要重新插值。如将一个连续的曲面从一种空间切分方式变为另一种空间切分方式,从TIN到栅格、栅格到TIN或矢量多边形到栅格。
3)现有的数据不能完全覆盖所要求的区域范围,需要插值。如将离散的采样点数据内插为连续的数据表面。
空间插值的理论假设是空间位置上越靠近的点,越可能具有相似的特征值;而距离越远的点,其特征值相似的可能性越小。然而,还有另外一种特殊的插值方法——分类,它不考虑不同类别测量值之间的空间联系,只考虑分类意义上的平均值或中值,为同类地物赋属性值。它主要用于地质、土壤、植被或土地利用的等值区域图或专题地图的处理,在“景观单元”或图斑内部是均匀和同质的,通常被赋给一个均一的属性值,变化发生在边界上。
连续表面空间插值的数据源包括:摄影测量得到的正射航片或卫星影象、卫星或航天飞机的扫描影像、野外测量采样数据(采样点随机分布或有规律的线性分布,沿剖面线或沿等高线)、数字化的多边形图、等值线图。
空间插值的数据通常是复杂空间变化有限的采样点的测量数据。如果采样点数据比较少的情况下,可以根据已知的导致某种空间变化的自然过程或现象的信息机理,辅助进行空间插值。但通常情况下,由于不清楚这种自然过程机理,往往不得不对该问题的属性在空间的变化作一些假设,例如假设采样点之间的数据变化是平滑变化,并假设服从某种分布概率和统计稳定性关系。
采样点的空间位置对空间插值的结果影响很大,理想的情况是在研究区内均匀布点。然而当区域景观大量存在有规律的空间分布模式时,如有规律间隔的数或沟渠,用完全规则的采样网络则显然会得到片面的结果,正是这个原因,统计学家希望通过一些随机的采样来计算无偏的均值和方差。但是完全随机的采样同样存在缺陷,首先随机的采样点的分布位置是不相关的,而规则采样点的分布则只需要一个起点位置,方向和固定大小的间隔,尤其是在复杂的山地和林地里比较容易。其次完全随机采样,会导致采样点的分布不均,一些点的数据密集,另一些点的数据缺少。图8-20列出空间采样点分布的几种选择。
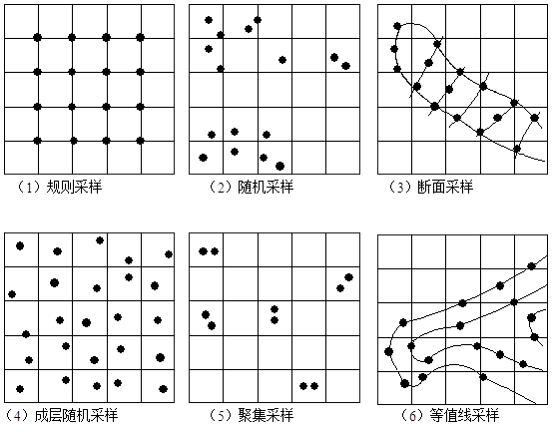
图8-20 各种不同的采样方式
规则采样和随机采样好的结合方法是成层随机采样,即单个的点随机的分布于规则的格网内。聚集采样可用于分析不同尺度的空间变化。规则断面采样常用于河流、山坡剖面的测量。等值线采样是数字化等高线图插值数字高程模型最常用的方法。
2. 空间插值方法
空间插值方法可以分为确定性和随机两种,确定性插值方法不提供预测值的误差检验。随机性插值法则考虑变量的随机性和用估计变异提供预测误差的评价。
此外,空间插值方法也可以分为整体插值和局部插值方法两类。整体插值方法用研究区所有采样点的数据进行全区特征拟合;局部插值方法是仅仅用邻近的数据点来估计未知点的值。表8-6显示了空间插值方法的分类。
表8-6 空间插值方法的分类
| 全局插值法 | 局部插值法 | ||
| 确定性 | 随机性 | 确定性 | 随机性 |
| 趋势面 (非精确) | 回归 (非精确) | 泰森(精确)、密度估算(非精确)、距离倒数权重(精确)、薄板样条(精确) | 克里金 (精确) |
整体插值方法通常不直接用于空间插值,而是用来检测不同于总趋势的最大偏离部分,在去除了宏观地物特征后,可用剩余残差来进行局部插值。由于整体插值方法将短尺度的、局部的变化看作随机的和非结构的噪声,从而丢失了这一部分信息。局部插值方法恰好能弥补整体插值方法的缺陷,可用于局部异常值,而且不受插值表面上其它点的内插值影响。
1)整体插值方法
边界内插方法
边界内插方法假设任何重要的变化发生在边界上,边界内的变化是均匀的,同质的,即在各方向都是相同的。这种概念模型经常用于土壤和景观制图,可以通过定义“均质的”土壤单元、景观图斑,来表达其它的土壤、景观特征属性。
实质上,边界内插方法的理论假设是:属性值z在“图斑”或景观单元内是随机变化的,不是有规律的;同一类别的所有“图斑”存在同样的类方差(噪声);所有的属性值都呈正态分布;所有的空间变化发生在边界上,是突变而不是渐变。在使用边界内插时,应仔细考虑数据源是否符合这些理论假设。
