当前位置:课程学习>>第八章 空间分析>>电子教案>>知识点四
知识点四:政策客体
趋势面分析
某种地理属性在空间的连续变化,可以用一个平滑的数学平面加以描述。思路是先用已知采样点数据拟合出一个平滑的数学平面方程,再根据该方程计算无测量值的点上的数据。这种只根据采样点的属性数据与地理坐标的关系,进行多元回归分析得到平滑数学平面方程的方法,称为趋势面分析,如图8-21所示。它的理论假设是地理坐标(x, y)是独立变量,属性值Z也是独立变量且是正态分布的,同样回归误差也是与位置无关的独立变量。

图8-21 由三阶趋势面模型生成的等值线图
多项式回归分析是描述长距离渐变特征的最简单方法。多项式回归的基本思想是用多项式表示线、面,按最小二乘法原理对数据点进行拟合。线或面多项式的选择取决于数据是一维的还是二维的。
变换函数插值
根据一个或多个空间参量的经验方程进行整体空间插值,也是经常使用的空间插值方法,这种经验方程称为变换函数。转换函数可以应用于其他独立变量,如温度、高程、降雨量和距海、植被的距离关系可以组合为一个超剩含水量的函数。地理位置及其属性可以尽可能多的信息组合成需要的回归模型,然后进行空间插值。但应该注意的一点是,必须清楚回归模型的物理意义。还要指出的是所有的回归转换函数都属于近似的空间插值。
整体插值方法通常使用方差分析和回归方程等标准的统计方法,计算比较简单。其它的许多方法也可用于整体空间插值,如傅立叶级数和小波变换,特别是遥感影象分析方面 ,但它们需要的数据量大。
2)局部插值方法
局部插值方法只使用邻近的数据点来估计未知点的值,如图8-21所示,包括几个步骤:定义一个邻域或搜索范围;搜索落在此邻域范围的数据点;选择表达这有限个点的空间变化的数学函数;为落在规则格网单元上的数据点赋值。重复这个步骤直到格网上的所有点赋值完毕。
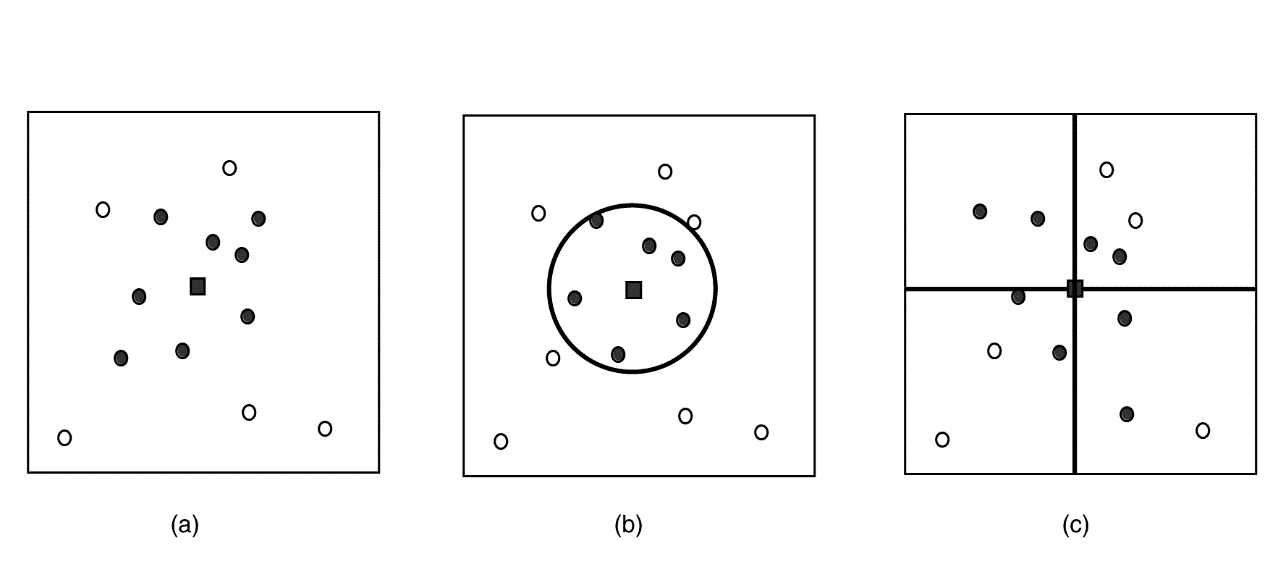
图8-21 搜索样本点的三种方法:(a)找到与估算点最邻近的点;(b)以半径搜索点;(c)用象限搜索点
使用局部插值方法需要注意的几个方面是:所使用的插值函数;邻域的大小、形状和方向;数据点的个数;数据点的分布方式是规则的还是不规则的。
最近邻点法:泰森多边形方法
泰森多边形(Thiessen,又叫Dirichlet 或Voronoi多边形)采用了一种极端的边界内插方法,只用最近的单个点进行区域插值。泰森多边形按数据点位置将区域分割成子区域,每个子区域包含一个数据点,各子区域到其内数据点的距离小于任何到其它数据点的距离,并用其内数据点进行赋值。连接所有数据点的连线形成Delaunay三角形,与不规则三角网TIN具有相同的拓扑结构,如图8-22所示。
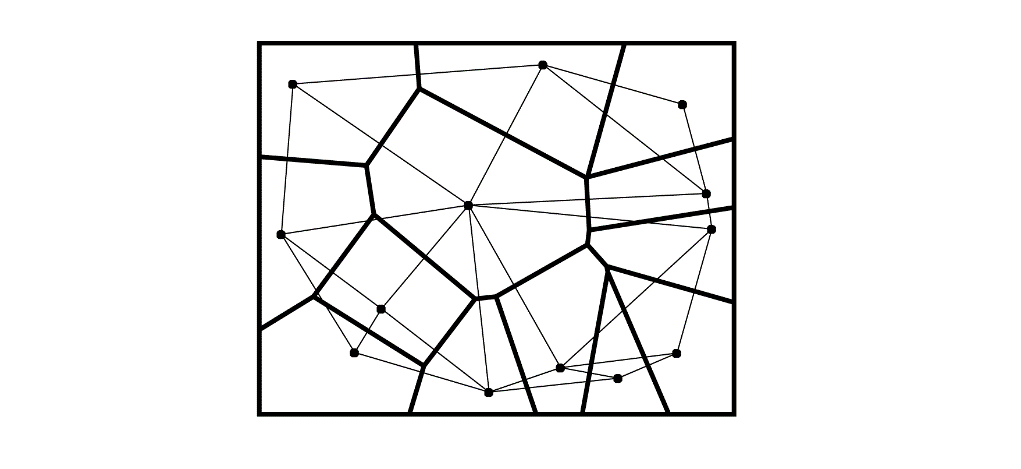
图8-22 由已知点和Delaunay三角形(细线表示的)插值生成的泰森多边形(粗线表示的)
GIS和地理分析中经常采用泰森多边形进行快速的赋值,实际上泰森多边形的一个隐含的假设是任何地点的气象数据均使用距它最近的气象站的数据。而实际上,除非是有足够多的气象站,否则这个假设是不恰当的,因为降水、气压、温度等现象是连续变化的,用泰森多边形插值方法得到的结果图变化只发生在边界上,在边界内都是均质的和无变化的。
移动平均插值方法:距离倒数插值
距离倒数插值方法综合了泰森多边形的邻近点方法和趋势面分析的渐变方法的长处,它假设未知点x0处属性值是在局部邻域内中所有数据点的距离加权平均值。距离倒数插值方法是加权移动平均方法的一种。距离倒数插值方法是GIS软件根据点数据生成栅格图层的最常见方法。距离倒数法计算值易受数据点集群的影响,计算结果经常出现一种孤立点数据明显高于周围数据点的“鸭蛋”分布模式,可以在插值过程中通过动态修改搜索准则进行一定程度的改进,如图8-23所示。
样条函数插值方法
在计算机用于曲线与数据点拟合以前,绘图员是使用一种灵活的曲线规逐段的拟合出平滑的曲线。这种灵活的曲线规绘出的分段曲线称为样条。与样条匹配的那些数据点称为桩点,绘制曲线时桩点控制曲线的位置。曲线规绘出的曲线在数学上用分段的三次多项式函数来描述这种曲线,其连接处有连续的一阶和二阶连续导数。
