当前位置:课程学习>>第十二章 遥感数字图像处理>>电子教案>>知识点三
知识点三:遥感图像增强
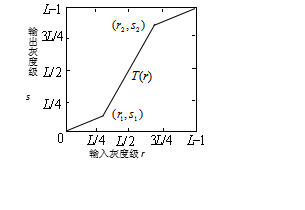
图1-5 分段线性变换
非线性增强指变换函数为线性方程以外的初等函数。
(1)对数变换
对数变换(Log Transformations)的一般表达式为:
(1-3)
其中,c是一个常数,并假设r≥0。此种变换使一窄带低灰度输入图像值映射为一宽带输出值,相对的是输入灰度的高调整值;也可以利用此种变换来扩展被压缩的高值图像中的暗像素,相对的是反对数变换的调整值。
(2) 指数变换
指数变换(Power-Law Transformations)的基本形式为:
(1-4)
其中,s,r分别为增强前后灰度值,a,b,c,d为根据需要确定的参数。
与对数变换的情况一样,指数函数也将把输入窄带暗值映射到宽带输出值;相反,输入高值时也成立。其效果与对数变换相反,可使高灰度区得以扩展。
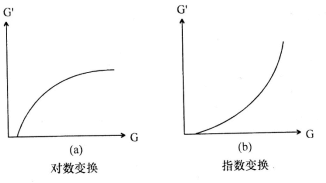
图1-6 对数与指数变换
3.2 空间滤波
空间域滤波是在空间域上对影像作局部检测的运算,以实现平滑和锐化的目的。具体作法是选定一卷积函数,又称“模板”,实际上是一个M×N影像。二维的卷积运算是在影像中使用模板来实现运算的(图1-7)。
(1-5)
从影像左上角开始开一与模板同样大小的活动窗口,影像窗口与模板像元的亮度值对应相乘再相加。假定模板大小为M*N,窗口为Φ(m,n),模板为t(m,n),则模板运算为:
将计算结果r(i,j)放在窗口中心的像元位置,成为新像元的灰度值。然后活动窗口向右移动一个像元,再按公式做同样的运算,仍旧把计算结果放在移动后的窗口中心位置上,依次进行,逐行扫描,直到全幅影像扫描一遍结束,则新影像生成。
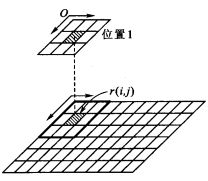
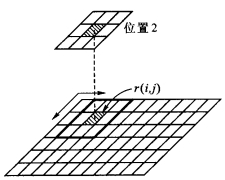
图1-7 空间滤波示意
即主要步骤为:
① 将模板在图中漫游,并将模板中心与图中某个像素位置重合;
② 将模板上系数与模板下对应像素相乘;
③ 将所有乘积相加;
④ 将和(模板的输出响应)赋给图中对应模板中心位置的像素。
1.平滑空间滤波器
平滑处理又称为平滑滤波,其主要作用是滤掉孤立的“单点噪声”和一些细节,以突出图像基本结构。可分为线性平滑和非线性平滑空间滤波器。
(1)均值滤波器
平滑线性空间滤波器的输出是包含在滤波掩膜邻域内像素的简单平均值。因此,这些滤波器也称为均值滤波器。平滑滤波器的概念非常直观,即用滤波掩膜确定的邻域内像素的平均灰度值去代替图像每个像素点的值,这种处理减小了图像灰度的“尖锐”变化。典型的随机噪声是由灰度级的尖锐变化组成,因此,常见的平滑处理应用就是减噪。
假定邻域大小为M×N,则均值平滑的计算公式为:
(1-6)
具体计算时常用3×3的模板作卷积运算,其模板为:
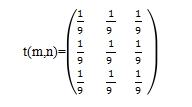
(2)中值滤波
是将每个像元在其为中心的邻域内取中间亮度值来代替该向像元值,以达到去尖锐“噪声”和平滑图像的目的。具体计算方法与均值平滑方法类似,仍采用活动窗口的扫描方法。取值时,将窗口内所有像元按亮度值的大小排序,取中间值作为中间像元的值。
2.锐化空间滤波器
为了突出图像的边缘、线状目标或某些亮度变化率大的部分,可采用锐化方法。锐化的方法很多,其中罗伯特梯度、索伯尔梯度和拉普拉斯算法较为常用。
(1)罗伯特梯度
梯度反映了相邻像元的亮度变化率,也就是说,图像中如果存在边缘,如湖泊、河流的边界、山脉和道路等,则边缘处有较大的梯度值。对于亮度值较平滑的部分,亮度梯度值较少。因此,找到梯度较大的位置,也就找到边缘,然后再用不同的梯度计算值代替边缘处像元的值,也就突出了边缘,实现了图像的锐化。
罗伯特梯度有2个,表示为:
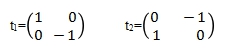
这个梯度相当于窗口2×2大小,用模板t1作卷积计算后取绝对值加上模板t2计算后的绝对值。计算出的梯度值放在左上角的像元位置上。这种算法的意义在于用交叉的方法检测出像元与其邻域在上下之间或左右之间或斜方向之间的差异,最终产生一个梯度影像,达到提取边缘信息的目的。
