参考答案

---

一、填空题

1． .   2. .  3..   4.可约.   5.1.

二．选择题

1.     2.    3.

三．计算题

1. .

2. 都是单根.

3.在复数域上的个根为

。在复数域上：

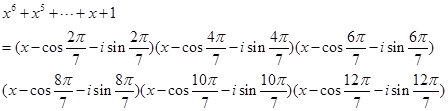
在实数域上：

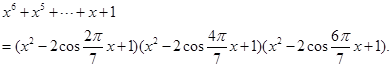
四.证明题

1.证明：存在,使得

,,所以

,

所以   .

2．令,则,取,由艾森斯坦判别法知，在有理数域上不可约.

3．一方面，若,显然有.另一方面，设,则有,使得.令,则有,,且与互素.于是有.因为必为非零常数，可设,则,.从而.