当前位置:课程学习>>第二章 一元多项式理论概述>>本章练习>>参考答案
参考答案
1. (1) ![]() ,
,![]() 。
。
(2) ![]() ,
,![]() 。
。
2. (1) ![]()
(2) ![]() ,
,![]() 。
。
3. (1)![]()
(2)![]()
4. (1) ![]() ,
,![]() ,
,![]() 。
。
(2) ![]() ,
,![]() ,
,![]() 。
。
5. (1) ![]() ,
,![]() 。
。
6. 设![]() 的常数项为
的常数项为![]() ,则
,则![]() 的常数项为
的常数项为![]() 。因此
。因此
![]() 。
。
7. 由于![]() ,所以
,所以![]() ,
,
![]() ,因此
,因此![]() 。
。
8. 因为![]() 互素,则存在
互素,则存在![]() ,使得
,使得![]() 。这说明
。这说明![]() 是零次多项式,从而
是零次多项式,从而![]() 。所以
。所以![]() 。
。
9. 设![]() ,则存在
,则存在![]() ,
,![]() 使
使![]() 。
。
所以![]() .又因
.又因![]() ,
,![]() ,所以
,所以![]() 是
是![]() 与
与![]() 的一个最大公因式。又因
的一个最大公因式。又因![]() ,
,![]() 都是首一多项式,故
都是首一多项式,故![]() 也是首一多项式,从而
也是首一多项式,从而
![]() 。
。
又如![]() ,则
,则![]() ,原等式仍成立。
,原等式仍成立。
10.(1) 当![]() 有3重因式
有3重因式![]() ,当
,当![]() 且
且![]() ,有
,有![]() 重因式
重因式![]() 。
。
(2) 当![]() 有4重因式
有4重因式![]() ,当
,当![]() 且
且![]() ,有
,有![]() 重因式
重因式![]() 。
。
11.![]()
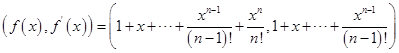
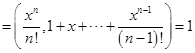 所以
所以![]() 无重根。
无重根。
12.(1)![]()
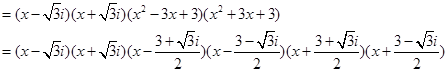
在复数域上的分解式:
![]() .
.
在实数域上的分解式:
![]() 。
。
(2)![]()
![]() 。
。
![]() ,
,
![]() ,
,
所以,![]() 在实数域与复数域的分解式分别为
在实数域与复数域的分解式分别为
![]()
![]() ;
;
![]()
![]()
![]() 。
。
13. 在复数域上的分解式:
![]() ;
;
在实数域上的分解式:
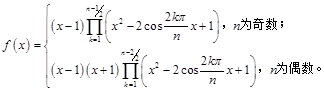
14.(1)应用综合除法易得![]() 是
是![]() 的二重根,
的二重根,![]() 不是有理根.
不是有理根.
(2)![]() 是
是![]() 的有理根.经验证,
的有理根.经验证,![]() 是
是![]() 的二重根.
的二重根.
15.(1)令![]() ,则
,则![]() ,取
,取![]() ,由艾森斯坦因判别法知,
,由艾森斯坦因判别法知,![]() 在有理数域上不可约.
在有理数域上不可约.
(2)令![]() ,展开后取
,展开后取![]() ,由艾森斯坦因判别法可得
,由艾森斯坦因判别法可得![]() 在有理数域上不可约.
在有理数域上不可约.
16.证明:![]() 是有理数域上的不可约多项式,于是
是有理数域上的不可约多项式,于是![]() 或者
或者![]() ,假定
,假定![]() ,令
,令![]() 是三次本原单位根,则
是三次本原单位根,则![]() ,且
,且![]() .
.
![]()
![]() ,矛盾,于是
,矛盾,于是![]() .
.
17. ![]()
![]()
![]()
对![]() ,令
,令![]() ,用艾森斯坦因判别法容易证明
,用艾森斯坦因判别法容易证明![]() 在有理数域上不可约,因此
在有理数域上不可约,因此![]() 在有理数域上的不可约因式为
在有理数域上的不可约因式为![]() 及
及![]() .
.
18.![]() 不可约,那么
不可约,那么![]() 或者
或者![]() ,假定
,假定![]() ,那么存在
,那么存在![]() ,使得
,使得![]() ,令
,令![]() 是
是![]() 与
与![]() 的公共复根,则
的公共复根,则![]() ,矛盾,于是
,矛盾,于是![]() .
.