高次方程的根  

讲二个问题：（1）三次方程求根公式；（2）四次方程求根公式

（1）三次方程求根公式  

代数学基本定理只是确定了次方程根的存在性，并没有给出求根的具体方法。一元二次方程的求根公式是众所周知的，对于一元三次方程求根公式在下面给出。

设一元三次方程

，                    （2.10.1）

令，得

，                       （2.10.2）

可见，三次方程均可化为无二次项的方程（2.10.2）。

设是方程（2.10.2）的一个根，讨论方程

。

设它的两个根分别是和，则

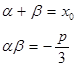                         （2.10.3）

由（2.10.3）得

，

即有

。             （2.10.4）

由（2.10.4）得

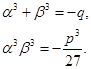
所以和是一元二次方程

的两个根。解此方程得

，

由此得         

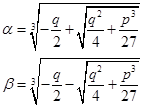
而  

。

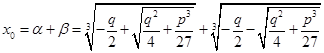这就是所谓的卡丹公式。

由于上式开三次方程给出三个值，三个值，因而共9个值，但这9个值不可能都是方程（2.10.2）的根，对于给定的值，只能取使得。

设是的三个值中的一个，是的立方根（），而是适合的值。

若是方程的根，则另外两个根是：。

现在讨论 

。

（1）若，这时是实数。实数的立方根有一个实数，两个共轭复数。

设是中的实数，是中的实数，

这时是方程的根（因为是实数）。另外两个根是：

 

             

这里显然有。所以三次方程的另外两个根是共轭复数。

（2）当时，。

设是的实数值，由知也是实数值，所以

              

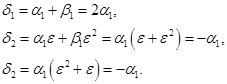
所以方程的三个根都是实数，且有两个根是相同的。

（3）当，卡丹公式中的方根下是一个负实数，所以与是一对共轭复数，所以与的值也是复数。由于实数系三次方程必有一个根为实数，设这个根为

，

因为为实数，也是实数，所以与为一元二次方程的根，即与为共轭复数。这时方程的另外两个根是

，

由于，则与都是实数，所以这时三次方程的根都是实数，而且这三个实数根是不同的。

刚才讨论的第（3）种情况，卡丹公式的实用价值不大，因为用卡丹公式计算平方根再计算立方根显然非常麻烦，也不易计算出来结果。

例2.10.1 解方程

解: 用代换得

这时，

，

即方程有一个实数根，两个共轭复数根

，。

所以，方程的根为

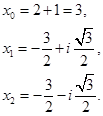
原方程的根为

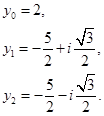
例2.10.2 解方程  。

解:    

      

所以       ，

于是

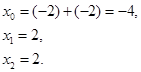
（2）四次方程的求根公式

下面再给出一元四次方程的求根公式。

设实系数四次方程为

利用代换 消去三次项得：

                     （2.10.5）

在上述方程加参数得

即    。

取使方括号里边是完全平方项，这时判别式，即

               （2.10.6）

方程（2.10.6）是的一元三次方程，由前述可以解出。

设是（2.10.6）式的一个解，则

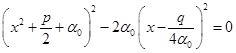
即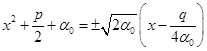         

上式可分解为两个二次方程

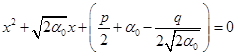              （2.10.7）

与 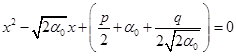                    （2.10.8）

由于方程（2.10.7）和（2.10.8）都是由恒等变换得到的，所以方程（2.10.7）和（2.10.8）的根都是方程（2.10.5）的根。至此四次方程的解法就算给出。

一个自然的问题：五次及五次以上一般方程是否有根式解？

在随后的300年间，数学家们的努力都是徒劳无功的。直到1770年，拉格朗日才第一个宣布“不可能用根式解四次以上方程”，但他却不能证明这个论断。1799年，鲁菲尼给出了一个证明，但它的证明是不完整的。1824年，年轻的阿贝尔给出了第一个严格的证明。阿贝尔虽然证明了“五次及五次以上的一般方程没有根式解”，但他并没有解决究竟哪些方程可用根式求解。伽罗瓦并不知道阿贝尔的工作，他深入研究了方程能用根式求解必须满足的本质条件，得到了代数方程能用根式解的充要条件是它所对应的群可解。至此五次及五次以上方程的根式解问题获得了圆满的解决，这是1831年的事。伽罗瓦工作是19世纪数学中最杰出的成就之一。伽罗瓦理论是代数学发展中的一个里程碑，代数学从此进入了近世代数的阶段。  

边学边练  

求下列方程的根

(1)

⑵ 。

答案 (1).. (2).  。