文本资源

 

 

学习指导

一、内容提要

1.基本概念

1）数域、一元多项式、多项式的根、多项式的整除、重因式；

2）最大公因式、多项式的互素、不可约多项式、本原多项式.

2.基本结论

1）带余除法；

2）最大公因式定理；

3）因式分解定理；

4）余数定理；

5）复系数多项式与实系数多项式的因式分解定理；

6）艾森斯坦因判别法。

3.基本方法

1）利用带余除法求多项式的商式与余式；

2）利用辗转相除法求最大公因式；

3）求整系数多项式的有理根；

4）会利用性质判断多项式的重因式；

5）利用艾森斯坦因判别法判断有理系数多项式不可约.

4.需要说明的问题

一元多项式的内容十分丰富。重点是整除与因式分解理论，最基本的结论是带余除法定理，最大公因式的存在表示定理与因式分解的唯一性定理。具体学习过程中，应注意以下几个方面的问题：

1）. 多项式的带余除法定理在多项式的整除性讨论中是基本的，要有完整的准确的理解。设，则满足

的中多项式往往会很多。因此仅仅由这么一个等式还不能断言被除的商是，余式是。

才可以说明被除的商是，余式是，进而都是唯一的。

2） 尽管在多项式整除概念的定义中，整除性是与系数域有关的。但是带余除法定理中商与余式的唯一性说明，多项式的整除性不因系数域扩张为某一个扩域而改变。这一结果允许我们在讨论整除性问题时把扩大到。而结论，无论是整除，还是不整除都适用于原来较小的范围。

3） 在求的最大公因式，并求使，而对进行辗转相除时，每一步必须原原本本地做带余除法，再由表示这些带余除法的等式求出。如果目的仅仅是求最大公因式，而并不需要求上述的，那么在进行辗转相除的过程中可以在任何一步把除式或者被除式用非零数乘之以化简运算。

4） 零多项式和零次多项式没有可约或者不可约的概念，也没有不可约分解的问题。

5） 多项式的可约与不可约概念与系数域有着绝对的关系。例如在有理数域上不可约，而在实数域上却可约；而在有理数域、实数域上都是不可约的，但在复数域上却是可约的。因此谈及不可约概念一定是与某个系数域相对应的。

6） 多项式的唯一因式分解定理只是在理论上肯定了分解的存在性和唯一性，并没有解决具体进行分解的方法。实际上判定一个具体的多项式是否是不可约的都是相当困难的。但是利用

因为的次数要大大的低于的次数，从而对进行不可约因式分解比对进行不可约因式分解要简单，甚至是由不可能而变为可能。这是因为与的不可约因式相同，相差的仅是不可约因式的次数。

7） 理解多项式的根的个数与其次数的关系；注意体会数域上的多项式在上的可约性与是否在中有根的关系与区别。可约未必有根，不可约的未必无根（一次多项式的情形）；有根未必可约(一次多项式的情形)，无根未必不可约。

8） 为了求多项式的根，人们发现了普遍适用的二次，三次乃至四次多项式的求根公式，但五次及五次以上的多项式都没有普遍适用的求根公式。

9） 设是有理系数多项式，,为有理数,是本原多项式，它的根与的根相同，因此求有理系数多项式的有理根可以转化为求整系数多项式的有理根。求整系数多项式的全部有理根的方法要注意：

（1）并不是说一定有有理根；

（2）若是有理根（互素），必是常数项的因子，必是首系数的因子。至于当是的因子，是的因子时，有理数究竟是不是的有理根尚需验证。也就是说的全部有理根都在集合

中，而这个集合中哪些有理数确是的根须经验证后方可知晓。不可误解为这个集合中的有理数都是的有理根。这个集合给出的仅仅是的有理根所在的一个范围。

 

二、精选例题解析  

例1 适合什么条件时，有。

解法1 待定系数法

如果     

则可设   

将上式右端展开，再比较同次项的系数，得

          

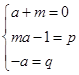
解得    

即当 时，。

解法2 带余除法

应用除法，求得商式及余式，令余式为零，从而得到所求条件。

 

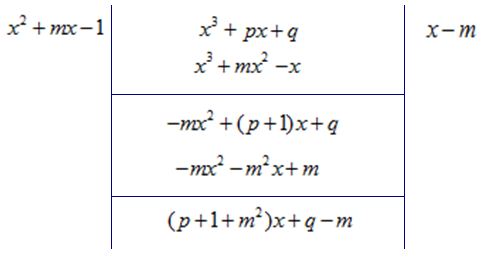
余式为    0。

于是得    

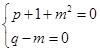
因此知，当时。

例2 求使其中

。

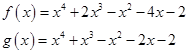解：辗转相除，然后反代，可得。

用等式写出来：

所以 而且

         

            

            

所以   。

例 3 证明：如果，且存在使得

        

则是与的一个最大公因式。

证明：设是与的任一公因式，则

          

又是与的公因式，从而由最大公因式的定义知，是与的一个最大公因式。

例4 设，若，则。

证明：由最大公因式的存在表示定理知，

存在，使得 

存在，使得 

所以

故。

例5 证明：如果，则

证明：因为，则有使得

 

  

故    

同理  

由例4的结论可知。

例6 已知是非负整数，证明：能被整除。

证明：设，则为的根，易知，从而

，

。

所以   ，

因为   ，

所以

。

注意：证明时利用了3次单位根及整除的性质。

例7 （北京大学，2002）设，证明：对任意的非负整数，

             。

证明：反证法

若，则存在多项式，使

于是  。

即是三次单位根，。

          ，矛盾。

因此。

注意：把所讨论的问题归结为方程根的讨论，利用三次单位根的性质获得了结论。本题也可直接证明。

例8 设，为正整数。

证明：如果，则。

证明：应用多项式的标准分解式，设

         

         

其中是互不相同的首系数为的不可约多项式，，

是非负整数。

 

如果   ，则   。

于是   ，从而  。

    注意：本题应用多项式的标准分解式来证，十分简捷。多项式的唯一分解定理与多项式的标准分解式虽然没有给出具体的一个多项式的因式分解，但具有重要的理论意义，是证明有关多项式性质的有利工具。

例9 求多项式的有理根。

解：为首相系数为的整系数多项式，故它的有理根都是整根，且都是常系数的因子。常数项的因子为，因为，所以与都不是的有理根。用综合除法可以看出只有是的有理根，而且是重根。

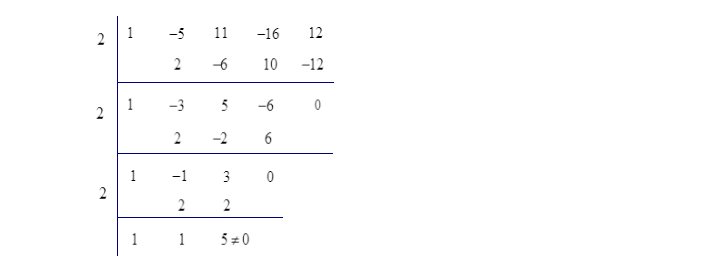
又，

而且    

所以都不是的根，同理也都不是的根。

注意：求有理根时，首先判定可能是有理根的范围是，但它们是不是有理根，需要进行判断，判断时用综合除法，这一点应特别强调。

例10 判别多项式

   

在有理数数域上是否可约。

解：令，则

  

取，则由艾森斯坦因判别法知，在有理数域上不可约，从而知

在有理数域上也不可约。

    注意:直接不能用艾森斯坦因判别法，但经过变换，则可化为应用艾森斯坦因判别法。这是判别整系数多项式不可约的一个常见方法。注意所用变换应是可逆的 ，这样，原多项式的可约性与变换后的多项式的可约性相同。

 

三、常见问题解析  

例1  判断下例说法是否正确？并说明理由。

(1)零多项式与零次多项式是一回事；

（2） 是复数域上的多项式；

（3）一个多项式的可约与不可约与所在数域无关，只与多项式的表达式有关。

解 （1）是错误的。零多项式是各项系数都是零的多项式，而零次多项式是

 ，这是两个不同的概念。

（2）错误。不是复数域上的多项式。因为若是复数域上的多项式，由代数基本定理，它在复数域上只有     根，事实上根是，无穷多个。这是矛盾的。因而， 是复数域上的多项式。

（3）错误。正确的说法是：一个多项式的可约与不可约与所在数域有关，也与多项式的表达式有关。如 在实数域上不可约，但在复数域上可约为  。

 

例 2 判断下例说法是否正确？并说明理由。

（1）如果 是多项式的一重根，则是多项式的二重根；

（2）设整系数多项式的次数为，当，有有理根与在有理数域上可约是等价的。

 

解 （1）错误。如，显然不是的根，但 是的一重根。错误的原因是缺少条件：如果是 与的一重根，则 是多项式 的二重根，这是正确的结论。

1. 等价的结论是错误的。正确的是：如果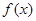有有理根，则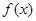在有理数域上可约。反之不成立。如 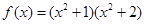在有理数域上可约，但在有理数域上无有理根。

 

例3 判断下列解法是否正确，并说明理由，同时给出正确的解法

1. 判断 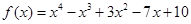在有理数域上是否可约？

 

解 因为不存在着素数满足艾森斯坦因判别法，所以多项式在有理数域是

可约。这是错误，原因是艾森斯坦因判别法只是一个充分条件，而非必要条件。即满足艾森斯坦因判别法可以得到结论，不满足时可能可约，也可能不可约。如

 不满足艾森斯坦因判别法，它在有理数域上不可约。

不满足艾森斯坦因判别法，它在有理数域上可约。

本题正确解法：令，则，   由艾森斯坦因判别法知， 在有理数域上不可约，从而在有理数域上也不可约。

 

例4 两个多项式的整除关系是否会因系数域的扩大而改变？

答 设 若在中不能整除，即在 中不存在 ，使得则在中应不能整除。这是因为：

若 因为中不能整除，所以从而在中应不能整除。

若，则在 中 ，且，但是，所以，因此 在中仍成立。于是，由的唯一性，在中仍不能整除。

例 5  引理2.4.1 的逆命题不成立，即若存在使得

也不能判断是的最大公因式。

例如 ，，于是有

显然不是的最大公因式。

但如果增加条件是公因式，则 是的最大公因式。

证明如下：因为是公因式；其次可设。于是若是公因式，则，从而。因此是的最大公因式。

 

例 6  如何理解多项式的唯一分解定理？

答 多项式的唯一分解定理只是在理论上肯定了分解的存在性和唯一性，并没有解决具体进行分解的方法。实际上判断一个具体的多项式是否是不可约的都相当的困难，甚至是不可能。对一些多项式的不可约分解就更是难上加难，还没有一个普遍适用的统一方法对多项式进行不可约分解。但是，推理2.6.4提供的方法使我们有可能对一些多项式进行不可约分解。这种方法只是使我们解决不可约分解的问题向前进了一步，但不是彻底解决，不论如何，这总是一个方法。