当前位置:课程学习>>第三章 行列式>>学习内容>>文本学习>>知识点八
知识点八:*拉普拉斯(Laplace)定理·行列式的乘法规则
这一节介绍行列式的拉普拉斯定理,这个定理可以看成是行列式按一行展开公式的推广.
首先我们把余子式和代数余子式的概念加以推广.
定义9 在一个![]() 级行列式
级行列式![]() 中任意选定
中任意选定![]() 行
行![]() 列
列![]() .位于这些行和列的交点上的
.位于这些行和列的交点上的![]() 个元素按照原来的次序组成一个
个元素按照原来的次序组成一个![]() 级行列式
级行列式![]() ,称为行列式
,称为行列式![]() 的一个
的一个![]() 级子式.在
级子式.在![]() 中划去这
中划去这![]() 行
行![]() 列后余下的元素按照原来的次序组成的
列后余下的元素按照原来的次序组成的![]() 级行列式
级行列式![]() 称为
称为![]() 级子式
级子式![]() 的余子式.
的余子式.
从定义立刻看出,![]() 也是
也是![]() 的余子式.所以
的余子式.所以![]() 和
和![]() 可以称为
可以称为![]() 的一对互余的子式.
的一对互余的子式.
例4 在四级行列式
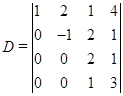
中选定第一、三行,第二、四列得到一个二级子式![]() :
:
![]() ,
,
![]() 的余子式为
的余子式为
![]() .
.
例5 在五级行列式
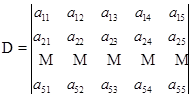
中
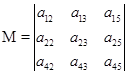
和
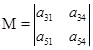
是一对互余的子式.
定义10 设![]() 的
的![]() 级子式
级子式![]() 在
在![]() 中所在的行、列指标分别是
中所在的行、列指标分别是![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() ,
,![]() ,
,![]() ,
,![]() .则
.则![]() 的余子式
的余子式![]() 前面加上符号
前面加上符号![]() 后称做
后称做![]() 的代数余子式.
的代数余子式.
例如,上述例1中![]() 的代数余子式是
的代数余子式是
![]() ,
,
上面例2中![]() 的代数余子式为
的代数余子式为
![]() .
.
因为![]() 与
与![]() 位于行列式
位于行列式![]() 中不同的行和不同的列,所以我们
中不同的行和不同的列,所以我们
有下述
引理 行列式![]() 的任一个子式
的任一个子式![]() 与它的代数余子式
与它的代数余子式![]() 的乘积中的每一项都是行列式
的乘积中的每一项都是行列式![]() 的展开式中的一项,而且符号也一致.
的展开式中的一项,而且符号也一致.
证明 我们首先讨论![]() 位于行列式
位于行列式![]() 的左上方的情形:
的左上方的情形:
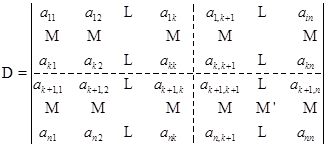 .
.
此时![]() 的代数余子式
的代数余子式![]() 为
为
![]() .
.
![]() 的每一项都可写作
的每一项都可写作
![]() ,
,
其中![]() 是
是![]() 的一个排列,所以这一项前面所带的符号为
的一个排列,所以这一项前面所带的符号为![]() ,
,![]() 中的每一项都可写作
中的每一项都可写作
![]() ,
,
其中![]() 是
是![]() 的一个排列,这一项在
的一个排列,这一项在![]() 中前面所带的符号是
中前面所带的符号是
![]() .
.
这二项的乘积是
![]() ,
,
前面的符号是
![]() .
.
因为每个![]() 比每个
比每个![]() 都大,所以上述符号等于
都大,所以上述符号等于
![]() .
.
因而这个乘积是行列式![]() 中的一项而且符号相同.
中的一项而且符号相同.
下面来证明一般情形.设子式![]() 位于
位于![]() 的第
的第![]() ,
,![]() ,
,![]() ,
,![]() 行;
行;![]() ,
,![]() ,
,![]() ,
,![]() 列,这里
列,这里
![]() ;
;![]() .
.
变动![]() 中行列式的次序使
中行列式的次序使![]() 位于
位于![]() 的左上角.为此,先把第
的左上角.为此,先把第![]() 行依次与第
行依次与第![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 行对换.这样经过了
行对换.这样经过了![]() 次对换而将第
次对换而将第![]() 行换到第一行.再将
行换到第一行.再将![]() 行依次与第
行依次与第![]() ,
,![]() ,
,![]() ,
,![]() 行对换而换到第二行,一共经过了
行对换而换到第二行,一共经过了![]() 次对换.如此继续进行.一共经过了
次对换.如此继续进行.一共经过了
![]()
次对换而把第![]() ,
,![]() ,
,![]() ,
,![]() 行依次换到第
行依次换到第![]() ,
,![]() ,
,![]() ,
,![]() 行.
行.
利用类似的列变换,可以将![]() 的列换到第
的列换到第![]() ,
,![]() ,
,![]() ,
,![]() 列.一共作了
列.一共作了
![]()
![]()
次列变换.
我们用![]() 表示这样的变换后所得的新行列式.那么
表示这样的变换后所得的新行列式.那么
![]()
![]()
由此看出,![]() 和
和![]() 的展开式中出现的项是一样的,只是每一项都差符号
的展开式中出现的项是一样的,只是每一项都差符号![]() .
.
现在![]() 位于
位于![]() 的左上角,所以
的左上角,所以![]() 中每一项都是
中每一项都是![]() 中的一项而且符号一致.但是
中的一项而且符号一致.但是
![]() .
.
所以![]() 中的每一项都与
中的每一项都与![]() 中一项相等而且符号一致.
中一项相等而且符号一致.
定理6(拉普拉斯定理) 设在行列式D中任意取定了![]() 个行.由这行元素组成的一切级子式与它们的代数余子式的乘积的和等于行列式
个行.由这行元素组成的一切级子式与它们的代数余子式的乘积的和等于行列式![]() .
.
证明 设![]() 中取定
中取定![]() 行后得到的子式为
行后得到的子式为![]() ,
,![]() ,
,![]() ,
,![]() ,它们的代数余子式分别为
,它们的代数余子式分别为![]() ,
,![]() ,
,![]() ,
,![]() ,定理要求证明
,定理要求证明
![]() .
.
根据引理,![]() 中每一项都是
中每一项都是![]() 中一项而且符号相同.而且
中一项而且符号相同.而且![]() 和
和![]() 无公共项.因此为了证明定理,只要证明等式两边项数相等就可以了.显然等式左边共有
无公共项.因此为了证明定理,只要证明等式两边项数相等就可以了.显然等式左边共有![]() 项,为了计算右边的项数,首先来求出
项,为了计算右边的项数,首先来求出![]() .根据子式的取法知道
.根据子式的取法知道
![]() .
.
因为![]() 中共有
中共有![]() 项,
项,![]() 中共有
中共有![]() 项.所以右边共有
项.所以右边共有
![]()
项.定理得证.
例3 在行列式
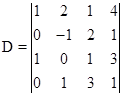
中取定第一、二行.得到六个子式:
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() .
.
它们对应的代数余子式为
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
根据拉普拉斯定理
![]()
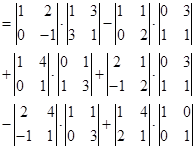
![]()
![]() .
.
从这个例子来看,利用拉普拉斯定理来计算行列式一般是不方便的.这个定理主要是在理论方面应用.
利用拉普拉斯定理可以证明
定理7 两个![]() 级行列式
级行列式
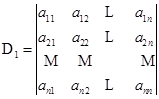
和
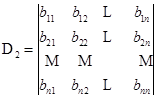
的乘积等于一个![]() 级行列式
级行列式
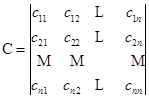
其中![]() 是
是![]() 的第
的第![]() 行元素分别与
行元素分别与![]() 的第
的第![]() 列对应元素乘积之和:
列对应元素乘积之和:
![]()
证明 作一个![]() 级行列式
级行列式
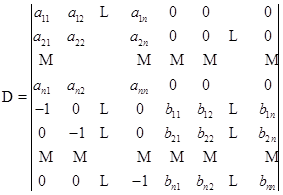 .
.
根据拉普拉斯定理,将![]() 按前
按前![]() 行展开.则因
行展开.则因![]() 中前
中前![]() 行中除去左上角那个
行中除去左上角那个![]() 级子式外,其余的
级子式外,其余的![]() 级子式都等于零.所以
级子式都等于零.所以
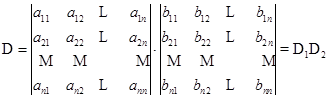
再依次将第![]() 行的
行的![]() 倍,第
倍,第![]() 行的
行的![]() 倍,
倍,![]() ,第
,第![]() 行的
行的![]() 倍加到第
倍加到第![]() 行,就得
行,就得
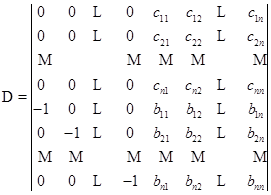 .
.
这个行列式的前![]() 行也只可能有一个
行也只可能有一个![]() 级行列式不为零,因此由拉普拉斯定理
级行列式不为零,因此由拉普拉斯定理
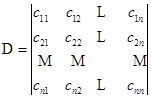
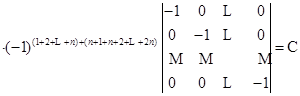
定理得证.
上述定理也称为行列式的乘法定理.它的意义到第四章§3中就完全清楚了.
