当前位置:课程学习>>第三章 行列式>>拓展资源>>拓展学习
文本资源
学习指导
一、内容提要
1.基本概念
1)排列的逆序数、奇排列与偶排列;
2)![]() 级行列式的定义、行列式元素的余子式与代数余子式.
级行列式的定义、行列式元素的余子式与代数余子式.
2.基本结论
1)行列式的基本性质;
2)行列式按一行(列)展开法则;
3)克拉默法则;
4)拉普拉斯定理。
3.基本方法
1)三角化法;
2)递推法;
3)加边法;
4)拆项法;
5)数学归纳法.
4.需要说明的问题
本章核心内容是行列式的定义和行列式的计算。一个应用是用行列式解方程组。具体学习过程中,应注意以下几个方面的问题:
1). 行列式的定义本书是一个交错和的定义方式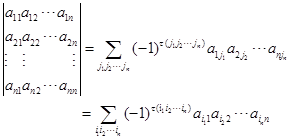 ,
,
故![]() 级行列式等于
级行列式等于![]() 项取不同行,不同列的
项取不同行,不同列的![]() 个元素的乘积
个元素的乘积![]() 的 代数和,每一项的正负号取决于组成该项的
的 代数和,每一项的正负号取决于组成该项的![]() 个元素的列下标所成排列的符号。即由
个元素的列下标所成排列的符号。即由![]() 确定。
确定。
应该注意:组成![]() 级行列式的矩阵应该是方阵,否则没有意义。
级行列式的矩阵应该是方阵,否则没有意义。
2)行列式的计算过程中,我们应该根据行列式的特点采取相应的方法,而不是盲目计算,这样可以避免浪费时间,有时可能不能获得结果。
计算行列式的主要方法有下列几种:1)三角化法;2)递推法;3)加边法;
4)拆项法;5)数学归纳法.其中1)、2)和5)是常用的方法,大家注意掌握。
实际计算过程中具体用那个方法方便,这要靠多练习,多留心,熟能生巧。
3)作为行列式在解线性方程组中的应用,得出了克拉默法则。可是它只能应用于方程个数与变量个数相等的情形,而且还要系数行列式不等于零,一般情形,需要用其它方法求解。这个结果只是在理论上有重要意义,实际计算时比较麻烦。
二、精选例题解析
例1写出四级行列式中所有带负号且包含因子![]() 项。
项。
解 四级行列式中包含因子![]() 项为
项为![]() ,其中
,其中![]() 是
是![]() 的排列。
的排列。![]() 的排列共有六个,所以这样的项共有六个。把
的排列共有六个,所以这样的项共有六个。把![]() 的每个排列
的每个排列![]() 代入使这些项具体化。由于
代入使这些项具体化。由于![]() 中
中![]() 是仅有的奇排列,所以四级行列式中带负号且含有因子
是仅有的奇排列,所以四级行列式中带负号且含有因子![]() 的项是
的项是![]()
例2 计算![]() 级行列式
级行列式
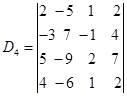
解 化三角法:先将1,3两列对换,得
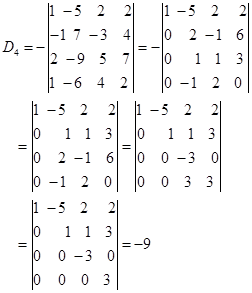
例 3 计算![]() 级行列式
级行列式
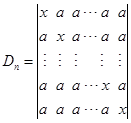
解法1 三角化法
将第1行乘以—1加到其它各行上,得
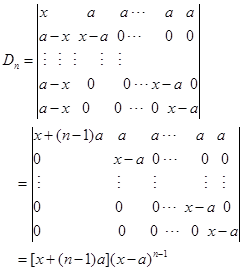
解法2 加边法
当![]() 时,
时,
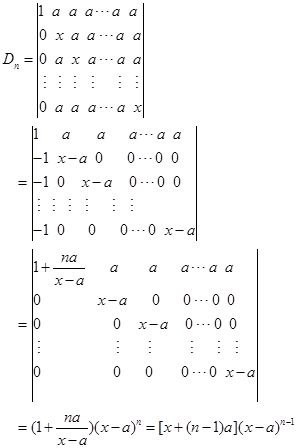
当![]() 时, 当
时, 当![]()
解法3 递推法
将![]() 的最后一列看成是两个数的和,即
的最后一列看成是两个数的和,即
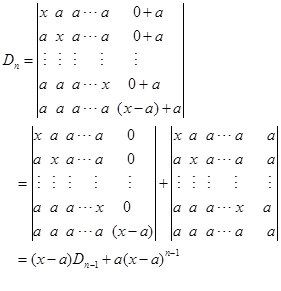
由此得递推公式![]()
以此递推下去,得
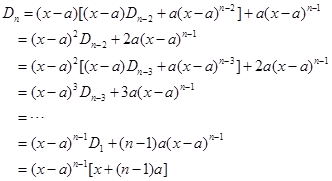
解法4 拆项法
将![]() 中的每个元素均看成两个数的和,利用行列式的性质,可分成
中的每个元素均看成两个数的和,利用行列式的性质,可分成![]() 个行列式,其中有多个行列式的值为零,即
个行列式,其中有多个行列式的值为零,即
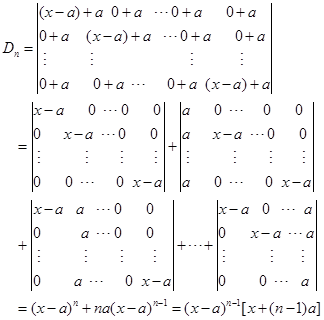
例4计算![]() 级行列式
级行列式
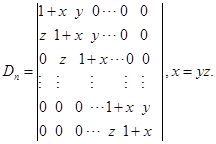 。
。
解 将行列式按第1行展开,得
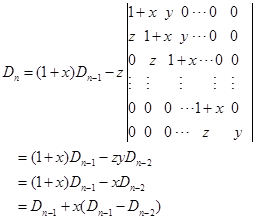
于是得![]()
从而有递推公式
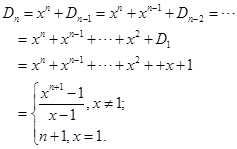
例5计算![]() 级行列式
级行列式
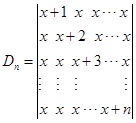
解 加边法
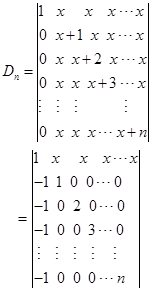
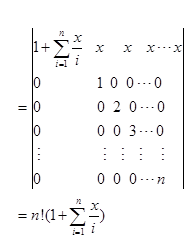
例6 证明
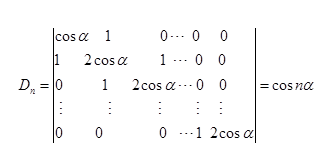
证明:用第二数学归纳法
当![]() 时,
时,![]() 结论成立。
结论成立。
假设对级数小于![]() 的行列式,结论成立,则按第
的行列式,结论成立,则按第![]() 行展开,得
行展开,得
![]()
由假设
![]()
代入前一个式子得![]()
故对一切自然数![]() 都成立。
都成立。
例7计算 ![]() 级行列式
级行列式
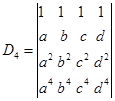
解 ![]() 不是范德蒙德行列式,但具有该行列式的特点,故可考虑构造
不是范德蒙德行列式,但具有该行列式的特点,故可考虑构造![]() 级的范德蒙德行列式,再利用范德蒙德行列式的结果,间接求出
级的范德蒙德行列式,再利用范德蒙德行列式的结果,间接求出![]() 。
。
构造5级范德蒙德行列式
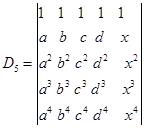
按第5列展开,得
![]()
其中![]() 的系数为
的系数为![]()
又利用范德蒙德行列式的结果得
![]()
其中![]() 的系数为
的系数为![]()
所以![]()
例8设![]() ,
,![]() ,
,![]() ,
,![]() 是数域
是数域![]() 中互不相同的数,
中互不相同的数,![]() ,
,![]() ,
,![]() ,
,![]() 是数域
是数域![]() 中任一组给定的数,用克拉默法则证明:存在唯一的数域
中任一组给定的数,用克拉默法则证明:存在唯一的数域![]() 上的多项式
上的多项式![]() 使
使
![]() ,
,![]() .
.
证明 设所求多项式为
![]() ,
,
利用所给条件有
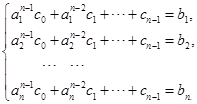
由于它的系数行列式
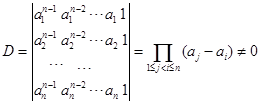
由克拉默法则,方程组有唯一解![]() ,所以存在唯一多项式
,所以存在唯一多项式
![]()
满足
![]()
例9 证明 平面上三条不同直线
![]()
相交于一点的充分必要条件是![]()
证明:必要性 设三条直线交于一点![]() ,故
,故![]() 是齐次线性方程组
是齐次线性方程组
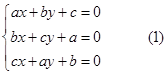
的一组的非零解,所以系数行列式![]() ,即
,即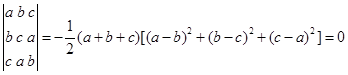
因为![]() 都是不相同的实数,所以必有
都是不相同的实数,所以必有![]()
充分性 若![]() 则由方程组(1)得
则由方程组(1)得
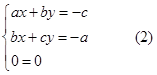
证明方程组(2)有唯一解。用反证法,设方程组(2)的解不唯一,则必有![]()
因为
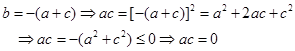
不妨设![]() ,则由
,则由![]() ;再由
;再由![]() ,这与三条不同直线假设矛盾,故
,这与三条不同直线假设矛盾,故![]() ,方程组(2)有唯一解,即方程组(1)有唯一解,亦即三条不同直线交于一点。
,方程组(2)有唯一解,即方程组(1)有唯一解,亦即三条不同直线交于一点。
例10 设![]() 互不相同的数,证明:下列线性方程组有唯一解,并求唯一解:
互不相同的数,证明:下列线性方程组有唯一解,并求唯一解:
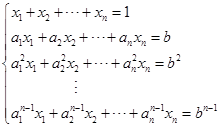
证明:方程组系数行列式
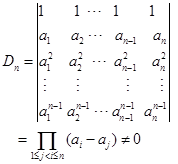
所以方程组有唯一解。
由范德蒙德行列式的结果,唯一解为
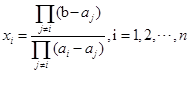 。
。


