参考答案

---

1.解 （1）

同解方程组为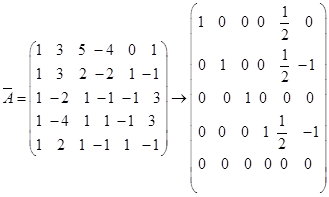

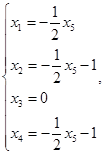
令，得，故特解为，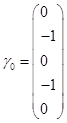

对应导出组为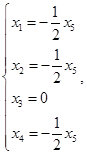令，得，故导出组基础解系为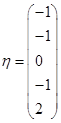，通解为，其中任意。

(2)

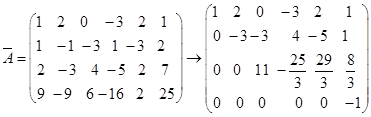
,方程组无解。

（3）

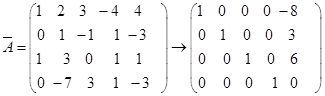
，方程组有唯一解为

（4）

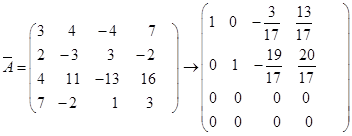
，方程组有无穷多解。

 同解方程组为

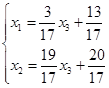
令，得，于是特解为

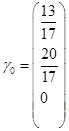
导出组对应方程组为

，

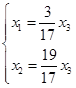令，得，导出组基础解系为

，

方程组的通解为任意。

2.（1）设，比较分量得

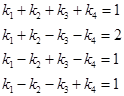
解此方程组得，所以

（2）同上可得。

3.证明 由题设，存在不全为零的使

下证。否则，若则不全为零使（*）式成立，这与线性无关条件矛盾，所以，由（*）式有。

4. 证明 设，得线性方程组

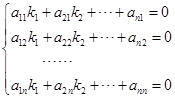
系数行列式的转置行列式，故齐次线性方程组只有零解，从而线性无关。

5. 证明 设

整理得

因为线性无关，所以有

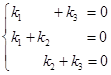
解得只有唯一零解，所以，，也线性无关.

6．证明 设是，，，中任意个线性无关的向量，下证都可由线性表示即可。

向量组线性相关，否则与向量组的秩是矛盾。故都可由线性表示，由的任意性，结论得证。

7.解 （1）因为，所以线性无关。

（2）直接证明可由线性表示，不能由线性表示，所以线性无关。再证明也可由表示，于是是由扩充的向量组的极大线性无关组。

8.解 （1）

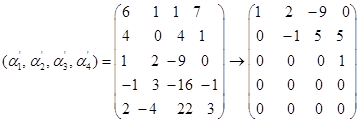
所以向量组的秩为3，且为极大线性无关组。

（2）同上得向量组的秩为3，所以为极大线性无关组。

9.证明 由假设，（I ）极大线性无关组也可由（II）的极大线性无关组表示，由教材的定理1的推理1可得的秩不超过的秩。

10.证明 的秩为,则。而的秩为，由假设　

向量，，，可被，，，线性表出，由上题结论有，

所以，因此，，，，线性无关。

11.证明 充分性 设任意维向量均可由，，线性表示，则单位，，，可由，，，线性表出，由上题知，，，线性无关。

必要性 设，，，线性无关，则，，，是的极大无关组，因此，任意维向量均可由，，线性表示。

12.证明 充分性 设，则系数矩阵的秩与增广矩阵的秩相等且都等于，方程组总有解。

必要性 设方程组对任何总有解，记，则方程组可改写为

这表示任意维向量总可由，，，表示，由上题结论知，，，线性无关，即方程组只有零解，所以。

13. 证明 由于，，，可由，，，线性表示，只需证 ，，，可由，，，线性表示，即可由，，，线性表示。

设，，，的极大线性无关组为，由于向量组，，，与 ，，，的秩相等，从而也是，，，极大线性无关组，故可由线性表示，从而可由，，，。

14.只需证明两向量组等价。由于可，，，线性表示，下证可由线性表示。由题设，

于是

即

可见，可由线性表示，故，，，与等价，从而秩相等。

15.解 （1）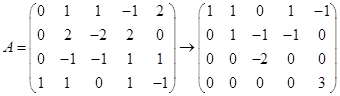

所以

（2）

16.解 （1）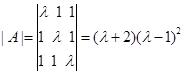

当，方程组有唯一解。利用克拉默法则，得

当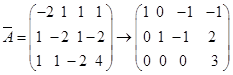，，，方程组无解。

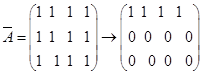当，，，方程组有无穷多解。同解方程组

，通解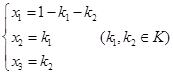

（2）

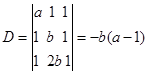
1. 当，方程组有唯一解利用克拉默法则有

 

2.当，，方程组无解。

3. 当，

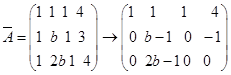
当，

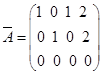
方程组统解为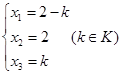

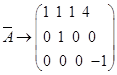当时，，，方程组无解。

17. （1）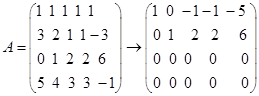

同解方程组为，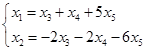

令，则得，故；令则得，故；令，则，故，所以基础解系为，，。全部解为是任意的。

（2）基础解系为。全部解为是任意的。

18. 解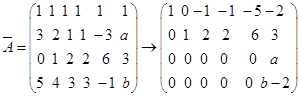

当 或，，方程组无解。

当，，方程组有无穷多解。同解方程组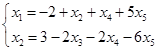

一般解为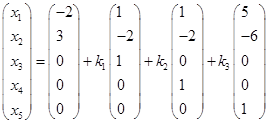，是任意的。

19. 证明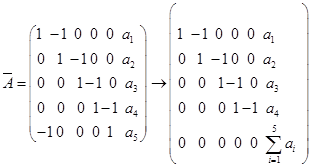

可见充分必要条件为，故原方程组有解的充分必要条件为。

20. 证明 由于等价的线性无关向量组含有向量个数相等。设（I）是齐次线性方程组的一个基础解系，又（II）是与（I）等价的线性无关向量组，那么（II）可以由（I）线性表示，从而是齐次线性方程组的线性无关解。

          齐次线性方程组的任意一个解都可由（I）线性表示，从而可由（II）线性表示，即证得（II）也是基础解系。

21.证明 设（I）：为齐次线性方程组的一个基础解系。（II）：

是齐次线性方程组的任意个线性无关解向量，那么，向量组（III）：秩仍为，所以（II）与（Ｉ）都是（ＩＩＩ）的极大线性无关组，所以（Ｉ）与（ＩＩ）等价，所以（ＩＩ）也是方程组的基础解系。

22. 设知，则有

所以，是的解。

.