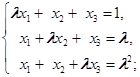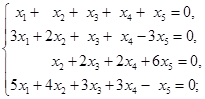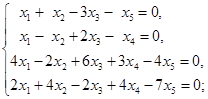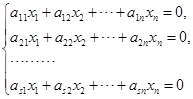. 用消元法解下列线性方程组

 

 

  

 

. 把向量表成向量，，，的线性组合:

，    ，

，   ，       

；

，   ，

 ，   ，

 .

. 证明：如果向量组，，，线性无关，而，，，，线性相关，则向量可以由，，，线性表出.

. , . 证明：如果，那么，，，线性无关.

5. 设，，线性无关，证明，，也线性无关.

6. 已知，，，的秩为，证明：，，，中任意个线性无关的向量都构成它的一极大线性无关组.

7. 设，，，，.

 证明，线性无关；

 把，扩充成一极大线性无关组.

8. 用消元法求下列向量组的极大线性无关组与秩：

 ，    ，

         ， ；

 ，     ，

        ，     ，

        .

9. 证明：如果向量组可以由向量组线性表出，那么的秩不超过的秩.

10. 设，，，是一组维向量，已知单位向量，，，可被它们线性表出，证明：，，，线性无关.

11. 设，，，是一组维向量，证明：，，，是线性无关的充分必要条件是任一维向量都可以被它线性表出.

12. 证明：方程组

对任何都有解的充分必要条件是系数行列式.

13. 已知，，，与，，，，，有相同的秩，证明：，，，与，，，，，等价.

14. 设，，，，证明：，，，与，，，有相同的秩.

15. 计算下列矩阵的秩：

 ；    ；

16. 讨论取什么值时下列方程组有解，并求解:

 

 

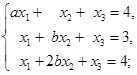
17. 求下列其次线性方程组的一个基础解系并用它表出全部解：

 

  

18. 取什么值时，线性方程组

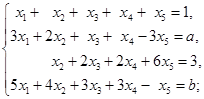
有解？在有解的情形，求一般解.

19. 设，，, , .证明：这方程组有解的充分必要条件为

                      .

在有解的情形，求出它的一般解.

20. 证明：与基础解系等价的线性无关向量组也是基础解系.

21. 设齐次方程组

的系数矩阵的秩为，证明：方程组的任意个线性无关的解都是它的一基础解系.

22. 证明：如果是一线性方程组的解，那么（其中）也是一个解。
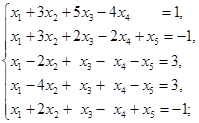
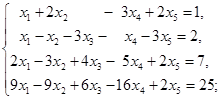
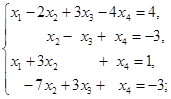
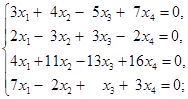
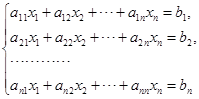
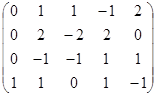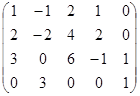