自 测 题

一.填空题

1.向量组则（       ）。

2.向量组的秩为（          )。

3.使向量组线性相关的值是（      ）。

4.含有个未知量的线性方程组的系数矩阵与增广矩阵的秩都是，则（    ）时，方程组有唯一的解；当（    ）时，方程组有无穷多解。

5. 含有个未知量的齐次线性方程组的系数矩阵的秩，则基础解系所含向量个数是（       ）。

二．选择题

1.在下列向量组中，线性无关的是（         ）

A.  B.  

C.     D. 

2. 向量组线性无关，向量可由线性表示，而向量不能由线性表示，则对任意常数，必有（      ）。

A．线性无关；  B. 线性相关；

C. 线性无关； D. 线性相关。

3.设是维向量组，下列命题中正确的是（      ）。

A. 如不能由线性表示，则线性无关；

B．如线性相关，不能由线性表示，则线性相关；

C.如中，任意个向量都线性无关，则线性无关；

D.零向量不能由线性表示。

4. 已知是的基础解系，则此方程组的基础解系还可选用（         ）。

A．；

B. 与等价的向量组；

C.与等秩的向量组；

D.。

三．计算题

1.求齐次线性方程组的基础解系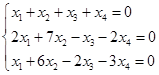

2.求方程组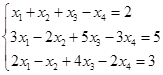

的一个特解及导出组的基础解系，并用基础解系及特解表示原方程组的全部解。

四．取何值时，下面方程组有解，并求解。

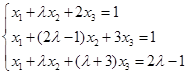
五． 证明题

1.若向量组线性相关，向量组线性无

关，证明：

（1）可由线性表示；

(2)的表示式是唯一的。

2.设齐次方程组

的系数矩阵的秩为，证明：方程组的任意个线性无关的解都是它的一基础解系。