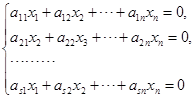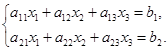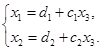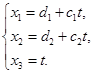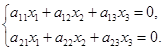在解决了线性方程组有解的判别条件之后，我们进一步来讨论线性方程组解的结构. 在方程组的解是唯一的情况下，当然没有什么结构的问题. 在有多个解的情况下，所谓解的结构问题就是解与解的关系问题. 下面我们将证明，虽然在这时有无穷多个解，但是全部的解都可以用有限多个解表示出来. 这就是本节要讨论的问题和要得到的主要结果. 下面的讨论当然都是对于有解的情况说的，这一点就不再每次都说明了.

上面我们提到，元线性方程组的解是维向量，在解不是唯一的情况下，作为方程组的解的这些向量之间有什么关系呢？我们先看齐次方程组的情形.设

是一齐次线性方程组，它的解所成的集合具有下面两个重要性质：

. 两个解的和还是方程组的解.

设与是方程组的两个解.这就是说，把它们代入方程组，每个方程成恒等式，即

，

.

把两个解得和

代入方程组，得

      

这说明确实是方程组的解.

. 一个解得倍数还是方程组的解.

设是方程组的一个解，不难看出还是方程组的解，因为

         .

从几何上看，这两个性质是清楚的. 在时，每个齐次方程表示一个过原点的平面. 于是方程组的解，也就是这些平面的交，如果不只是原点的话，就是一条过原点的直线或一个过原点的平面. 以原点为起点，而端点在这样的直线或平面上的向量显然具有上述的性质.

对于齐次线性方程组，综合以上两点即得，解的线性组合还是方程组的解. 这个性质说明了，如果方程组有几个解，那么这些解的所有可能的线性组合就给出了很多的解. 基于这个事实，我们要问：齐次线性方程组的全部解是否能够通过它的有限的几个解的线性组合给出来？答案是肯定的. 为此，我们引入下面的定义.

定义 齐次线性方程组的一组解 称为的一个基础解系，如果

的任意一个解都能表成的线性组合；

线性无关.

应该注意，定义中的条件是为了保证基础解系中没有多余的解. 事实上，如果线性相关，也就是其中有一个可以表成其他的解的线性组合，譬如说，可以表成的线性组合，那么显然也具有性质.

现在就来证明，齐次线性方程组的确有基础解系.

定理   在齐次线性方程组有非零解的情况下，它有基础解系，并且基础解系所含解的个数等于，这里表示系数矩阵的秩（以下将看到，也就是自由未知量的个数）.

定理的证明事实上就是一个具体找基础解系的方法.

证明  设方程组的系数矩阵的秩为，无妨设左上角的级子式不为零. 于是按上一节最后的分析，方程组可以改写成

                 

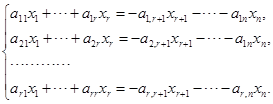
如果，那么方程组没有自由未知量，方程组的右端全为零. 这时方程组只有零解，当然也就不存在基础解系. 以下设.

我们知道，把自由未知量的任意一组值代入，就为唯一地决定了方程组——也就是方程组的一个解.换句话说，方程组的任意两个解，只要自由未知量的值一样，这两个解就完全一样. 特别地，如果在一个解中，自由未知量的值全为零，那么这个解一定就是零解.

在中我们分别用组数

，，，                   

来代自由未知量，就得出方程组——也就是方程组的个解：

                     

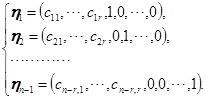
我们现在来证明，就是一个基础解系. 首先证明线性无关. 事实上，如果

，

即

比较最后个分量，得

因此，线性无关.

再证明方程组的任一个解都可以由线性表出. 设

                  

是的一个解. 由于是的解，所以线性组合

                   

也是的一个解. 比较和的最后个分量得知，自由未知量有相同的值，从而这两个解完全一样，即

               

这就是说，任意一个解都能表成的线性组合. 综合以上两点，我们就证明了确为方程组的一个基础解系，因而齐次线性方程组的确有基础解系. 至于其他的基础解系，由定义，一定与这个基础解系等价，同时它们又都是线性无关的，因而有相同个数的向量. 这就是定理的第二个部分.

    下面来看一般线性方程组的解的结构. 如果把一般线性方程组

                 

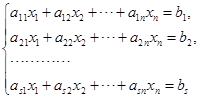
的常数项换成，就得到齐次方程组. 方程组称为方程组的导出组. 方程组的解与它的导出组的解之间有密切的关系：

.线性方程组的两个解的差是它的导出组的解.

设，是方程组的两个解，即

，  .

它们的差是

显然有

.

这就是说，是导出组的一个解.

.线性方程组的一个解与它的导出组的一个解之和还是这个线性方程组的一个解.

设是的一个解，即

                   .

又设 是导出组的一个解，即   

                   .

显然

        .

由这两点我们很容易证明下面的定理：

定理  如果是方程组的一个特解，那么方程组的任意一个解都可以表成

，                          

其中是导出组的一个解. 因此，对于方程组的任意一个特解，当取遍它的导出组的全部解时，就给出的全部解.

    证明  显然

，

由上面的，是导出组的一个解，令

，

就得到定理的结论. 既然的任意一个解都能表成的形式，由，在取遍的全部解的时候，

就取遍的全部解.

定理说明了，为了找出一线性方程组的全部解，我们只要找出它的一个特殊解以及它的导出组的全部解就行了. 导出组是一个齐次方程组，在上面我们已经看到，一个齐次线性方程组的解的全体可以用基础解系来表出. 因此，根据定理我们可以用导出组的基础解系来表出一般线性方程组的一般解：如果是方程组的一个特解，是其导出组的一个基础解系，那么的任一个解都可以表成

推论  在方程组有解的条件下，解是唯一的充分必要条件是它的导出组只有零解

证明  充分性：如果方程组有两个不同的解，那么它们的差就是导出组的非零解. 因之，如果导出组只有零解，那么方程组有唯一解.

必要性：如果导出组有非零解，那么这个解与方程组的一个解（因为它有解）的和就是的另一个解，也就是说，不止一个解. 因之，如果方程有唯一的解，那么它的导出组只有零解.

线性方程组的理论与解析几何中关于平面与直线的讨论有密切的关系. 我们来看线性方程组

                    

中每个方程表示一个平面，线性方程组有没有解的问题就相当于这两个平面有没有交点的问题. 我们知道，两个平面只有在平行而不重合的情形没有交点. 的系数矩阵与增广矩阵分别是

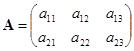      与，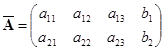

它们的秩可能是或者. 有三种可能的情形：

.的秩，的秩. 这就是的两行成比例，因而这两个平面平行. 又因为的两行也成比例，所以这两个平面重合. 方程组有解.

.的秩，的秩. 这就是说两个平面平行而不重合. 方程组无解.

.的秩. 这时的秩一定也是. 在几何上就是这两个平面不平行，因而一定相交. 方程组有解.

下面来看看线性方程组的解的几何意义. 设矩阵的秩为，这时一般解中有一个自由未知量，譬如说，一般解的形式为

                           

从几何上看，两个不平行的平面相交成一条直线. 把改写一下就是直线的点向式方程

.

如果引入参数，令，就成为

                         

就是直线的参数方程.

的导出方程组是

                     

从几何上看，这是两个分别与中平面平行的且过原点的平面，因而它们的交线过原点且与直线平行. 既然与直线平行，也就是有相同的方向，所以这条直线的参数方程就是

                             

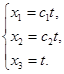
与正说明了线性方程组与它导出方程组的解之间的关系.