当前位置:课程学习>>第五章 矩阵>>本章练习>>参考答案
参考答案
1.解 (1)
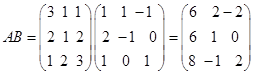
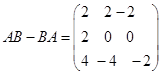
(2)
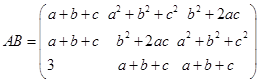
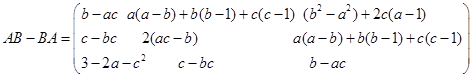
2.解
(1) 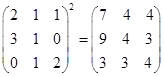 ;
;
(2) 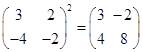 ;
;
(3) 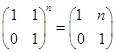 ;
;
(4) 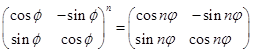 ;
;
(5) 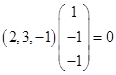 ,
,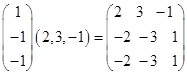 ;
;
(6) 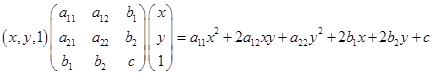 ;
;
(7) 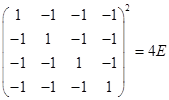 ,当
,当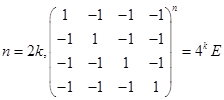 ;
;
当![]() 时,
时,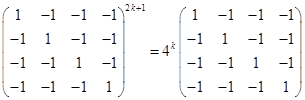
(8)
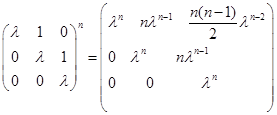 .
.
3.解(1)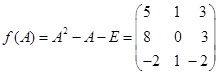
(2)![]()
4.解 (1)设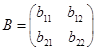 ,
,
则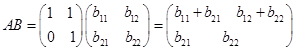
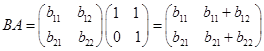
由![]() ,得
,得![]() ,所以所有与
,所以所有与![]() 可交换的矩阵为形如
可交换的矩阵为形如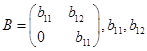 为任意数。
为任意数。
(2)与(1)同样做法,可得所有与![]() 可交换的矩阵为形如
可交换的矩阵为形如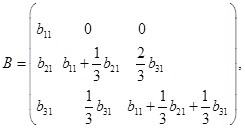 其中
其中![]() 为任意数。
为任意数。
(3)与(1)同样做法,可得所有与![]() 可交换的矩阵为形如
可交换的矩阵为形如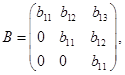
其中![]() 为任意数。
为任意数。
5.证明 设![]() 与
与![]() 可交换
可交换
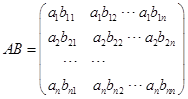
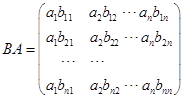
由![]() ,得
,得![]()
因当![]() 时,
时,![]() ,此时有
,此时有![]() ,于是得
,于是得![]() 为对角矩阵,即与
为对角矩阵,即与![]() 可交换的矩阵为对角矩阵。
可交换的矩阵为对角矩阵。
6.证明 设![]() 是与
是与![]() 可交换的
可交换的![]() 级矩阵,将
级矩阵,将![]() 分块为
分块为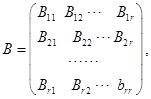
其中![]() 是
是![]() 矩阵。
矩阵。
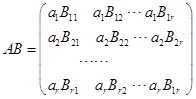
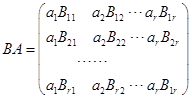
由![]() ,得
,得![]()
![]() 时,
时,![]() ,因此当
,因此当![]() 时,
时,![]() 。即
。即![]() 为准对角矩阵。
为准对角矩阵。
 ,其中
,其中![]() 是
是![]() 级矩阵。
级矩阵。
7. 证明 (1)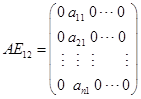
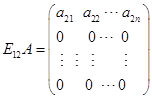
由![]() ,得当
,得当![]() 时,
时,![]() 且
且![]() 。
。
(3)如果![]() 与所有矩阵可交换,则
与所有矩阵可交换,则![]() 与所有
与所有![]() 可交换,由(2)可得当
可交换,由(2)可得当![]() 时,
时,![]() ,且
,且![]() ,对所有的
,对所有的![]() 皆成立。所有
皆成立。所有![]() 。
。
8.证明 ![]()
![]()
9. 证明 如果![]() ,即
,即
![]()
于是得![]() 。
。
反之,如果![]() ,则
,则
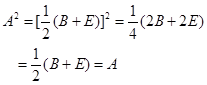
10. 证明 设![]() ,
,
则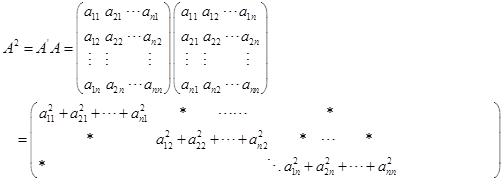
如果![]() ,则
,则
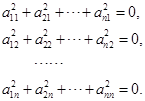
又![]() 皆为实数,所以
皆为实数,所以![]() 于是有
于是有![]() 。
。
11. 证明 设![]() 级矩阵
级矩阵![]() ,
,![]() 皆为对称矩阵,则
皆为对称矩阵,则
![]() ,即
,即![]() 可交换。
可交换。
反之,若![]() 对称,且
对称,且![]() 可交换,则
可交换,则
![]() ,即
,即![]() 为对称矩阵。
为对称矩阵。
12. 证明 显然有![]() ,
,![]() 是对称矩阵,而
是对称矩阵,而![]() 为反对称矩阵。
为反对称矩阵。
13.证明 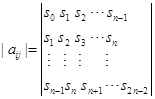
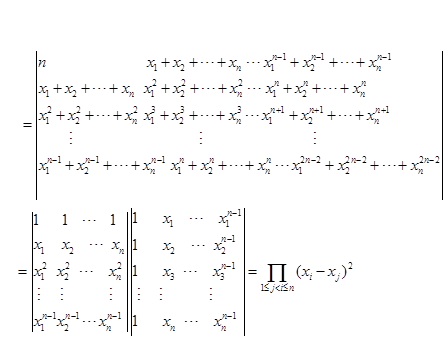
14. 必要性 将![]() 列分块
列分块![]() ,由
,由![]() 得
得![]() ,即
,即![]() 是
是![]() 的解向量,又
的解向量,又![]() 因此
因此![]() 中至少有一个不为零
中至少有一个不为零![]() 即方程组
即方程组![]() 有非零解
有非零解![]() 于是
于是![]() 。
。
充分性 如果![]() ,则方程组
,则方程组![]() 有非零解
有非零解![]() 令
令![]() ,则
,则![]() 且有
且有![]()
15. 证明 令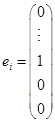 ,即
,即![]() 表第
表第![]() 行元素为1,其余元素为0,
行元素为1,其余元素为0,![]() ,则
,则
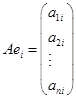
即![]() 于是有
于是有![]() 。
。
16. 证明 (1)因![]() 即
即![]() 中存在一个
中存在一个![]() 级子式不为零,不仿设
级子式不为零,不仿设![]() 中前
中前![]() 列所构成的
列所构成的![]() 级子式不为0,设
级子式不为0,设![]() ,
,![]() 为
为![]() 矩阵,
矩阵,![]() 为
为![]() 矩阵,且
矩阵,且![]() ,由
,由![]() ,得
,得![]() 。又
。又![]() 为
为![]() 可逆矩阵,所以
可逆矩阵,所以![]()
(2)由![]() ,得
,得![]() ,由(1),有
,由(1),有![]() ,即
,即![]() 。
。
17. 证明 设![]()
![]()
![]() 分别是
分别是![]() 的列向量组的极大线性无关组,则
的列向量组的极大线性无关组,则![]() 的每一列向量
的每一列向量![]() 可由
可由![]() 线性表出,所以
线性表出,所以
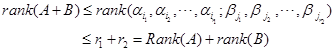
18. 证明 设![]() ,即
,即![]() 是
是![]() 的列向量。由
的列向量。由![]() ,得
,得![]() 即
即![]() 是方程组
是方程组![]() 的解向量。又方程组
的解向量。又方程组![]() 的解向量组的秩为
的解向量组的秩为![]() ,所以有
,所以有![]() ,
,
所以 ![]() 。
。
19. 证明
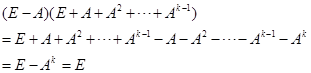
所以![]()
20. 解(1)用伴随矩阵求![]()
(2)用初等矩阵求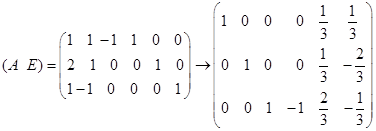
所以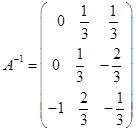
(3)用(2)同样方法,得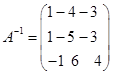
(4)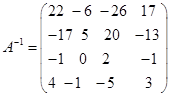
(5) 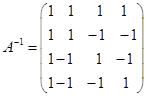
(6) 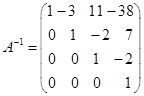 。
。
21. 解 将![]() 作适当分块,设
作适当分块,设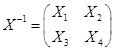 ,其中
,其中![]() 与
与![]() 同型,
同型,![]() 与
与![]() 同型,则
同型,则
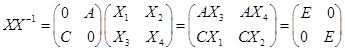
所以 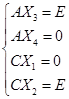
由此得 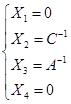
于是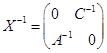 。
。
22. 解 设![]() ,
,
其中 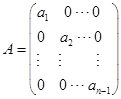 ,
,![]()
由习题21,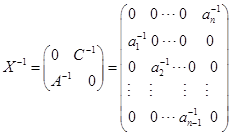 。
。
23. 解 (1)
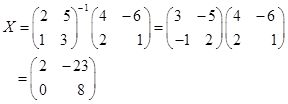
(2)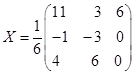
(3)![]()
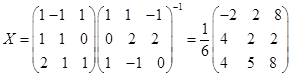
24. 证明 (1)因为![]() 可逆,且
可逆,且![]() ,所以
,所以
![]() ,即
,即![]() 对称。
对称。
如果![]() ,则
,则![]() ,即
,即![]() 反对称。
反对称。
(2) 设![]() 为
为![]() 级方阵,且
级方阵,且![]() ,
, ![]() 为奇数,则
为奇数,则
![]() ,所以
,所以![]() ,故
,故![]() 不可逆。
不可逆。
25. 证明 因为![]() ,所以
,所以 ![]() 。
。
如果![]() ,则有
,则有![]()
如果![]() ,若要结论成立,即要证
,若要结论成立,即要证![]() 。
。
当![]() ,则
,则![]() ,结论显然成立。
,结论显然成立。
当![]() ,若
,若![]() ,则
,则![]() 可逆,此时
可逆,此时
![]() ,与假设矛盾。因此,当
,与假设矛盾。因此,当![]() 时,
时,![]() 。
。
因此有![]() 。
。
26. 证明 (1)当![]() ,即
,即![]() 可逆,
可逆,![]() ,所以
,所以![]() 可逆,因此
可逆,因此![]()
(2)当![]() ,
,![]() ,
,
所以
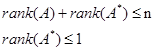
又![]() ,即
,即![]() 中存在一个
中存在一个![]() 子式不为0,所以
子式不为0,所以![]() 中至少有一个元素
中至少有一个元素![]() 的代数余子式不为0,所以
的代数余子式不为0,所以![]() ,所以
,所以![]() ,所以
,所以![]() 。
。
(3)当![]() ,即
,即![]() 中所有
中所有![]() 子式都为0。从而
子式都为0。从而![]() 中所有元素
中所有元素![]() 的代数余子式都为0,故
的代数余子式都为0,故![]() ,所以
,所以![]() 。
。
27. 解 (1)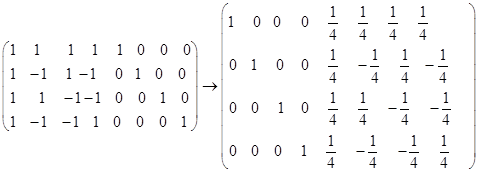
所以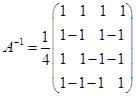
(2)设![]()
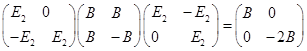
上两边取逆,得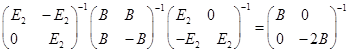
所以
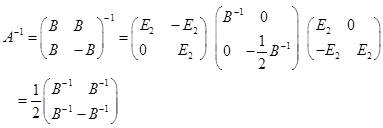
由![]() ,得
,得![]()
于是有![]() 。
。
.