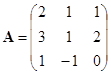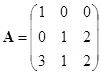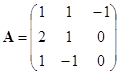当前位置:课程学习>>第五章 矩阵>>本章练习
![]() . 设
. 设
![]()
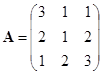 ,
,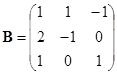 ;
;
![]()
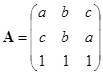 ,
,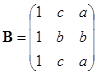 ,
,
计算 ![]() ,
,![]() .
.
![]() . 计算:
. 计算:
![]()
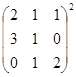 ;
; ![]()
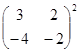 ;
;
![]()
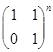 ;
; ![]()
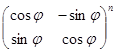 ;
;
![]()
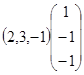 ,
,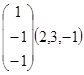 ;
;
![]()
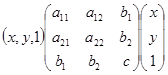 ;
;
![]()
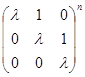 .
.
![]()
![]() ,
,![]() .
.
试求![]() .
.
![]()
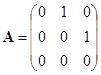 .
.
求与![]() 所有可交换的矩阵.
所有可交换的矩阵.
![]() . 设
. 设
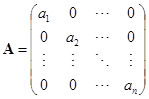 ,其中
,其中![]() 当
当![]()
![]() .
.
![]() . 设
. 设
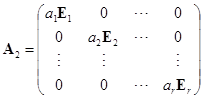 ,其中
,其中![]() 当
当![]()
![]() .
.
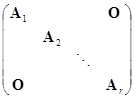 ,
,
其中![]() 是
是![]() 级矩阵
级矩阵 ![]() .
.
![]() . 用
. 用![]() 表示
表示![]() 行
行![]() 列的元素为
列的元素为![]() ,而其余元素全为零的
,而其余元素全为零的![]() 矩阵,而
矩阵,而![]() . 证明:
. 证明:
![]() 如果
如果![]() ,那么当
,那么当![]() 时
时![]() ,当
,当![]() 时;
时; ![]() ;
;
![]() 如果
如果![]() ,那么当
,那么当![]() 时
时![]() ,当
,当![]() 时
时![]() ,且
,且![]() ;
;
![]() 如果
如果![]() 与所有的
与所有的![]() 级矩阵可交换,那么
级矩阵可交换,那么![]() 一定是数量矩阵,即
一定是数量矩阵,即![]() .
.
![]() . 矩阵
. 矩阵![]() 称为对称的,如果
称为对称的,如果![]() . 证明:如果
. 证明:如果![]() 是实对称矩阵且
是实对称矩阵且![]() ,那么
,那么![]() .
.
![]() . 设
. 设![]() ,
,![]() 都是
都是![]() 的对称矩阵,证明:
的对称矩阵,证明:![]() 也对称当且仅当
也对称当且仅当![]() ,
,![]() 可交换.
可交换.
![]() . 矩阵
. 矩阵![]() 称为反对称,如果
称为反对称,如果![]() . 证明:任一
. 证明:任一![]() 矩阵都可表为一对称阵与一反对称阵之和.
矩阵都可表为一对称阵与一反对称阵之和.
![]() . 设
. 设![]() ,
,![]() ;
;![]() ,
,![]() . 证明:
. 证明:
![]() .
.
![]() . 设
. 设![]() 是
是![]() 矩阵,如果对任一
矩阵,如果对任一![]() 维向量
维向量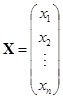 都有
都有![]() ,那么
,那么![]() .
.
![]() 如果
如果![]() ,那么
,那么![]() ;
;
![]() 如果
如果![]() ,那么
,那么![]() .
.
![]() . 证明
. 证明
秩![]()
![]() 秩
秩![]()
![]() 秩
秩![]() .
.
![]() . 设
. 设![]() ,
,![]() 为
为![]() 矩阵. 证明:如果
矩阵. 证明:如果![]() ,那么
,那么
秩![]()
![]() 秩
秩![]()
![]() .
.
![]() . 证明:如果
. 证明:如果![]() ,那么
,那么
![]() .
.
![]() . 求
. 求![]() ,设
,设
![]()
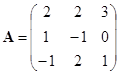 ;
; ![]()
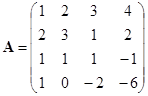 ;
;
![]()
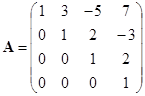 ; 6)
; 6)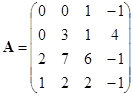 。
。
![]() . 设
. 设
![]() ,
,
![]() . 设
. 设
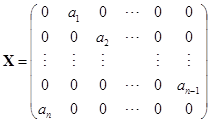 ,
,
其中![]()
![]() ,求
,求![]() .
.
![]() . 求矩阵
. 求矩阵![]() .设
.设
![]()
![]() ;
;
![]()
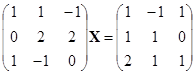 ;
;
![]()
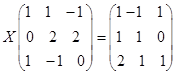 .
.
![]() . 证明:
. 证明:
![]() 如果
如果![]() 可逆对称(反对称),那么
可逆对称(反对称),那么![]() 也对称(反对称);
也对称(反对称);
![]() 不存在奇数级的可逆反对称阵.
不存在奇数级的可逆反对称阵.
![]() . 证明:
. 证明:
![]() ,
,
![]() . 证明:如果
. 证明:如果![]() 是
是![]() 矩阵(
矩阵(![]() ),那么
),那么
秩![]()
![]()
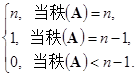
![]() . 用两种方法求
. 用两种方法求
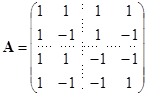
的逆矩阵,![]() 用初等变换;
用初等变换;
![]() 按
按![]() 中的划分,利用分块乘法的初等变换. (注意各小块矩阵的特点.)
中的划分,利用分块乘法的初等变换. (注意各小块矩阵的特点.)

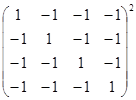
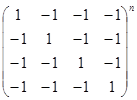 ;
;