当前位置:课程学习>>第五章 矩阵>>本章练习>>自测题
自 测 题
一.填空题
1.设![]() 是
是![]() 矩阵,
矩阵,![]()
![]() 矩阵,则
矩阵,则![]() 是( )行( )列矩阵。
是( )行( )列矩阵。
2. ![]() 阶方阵
阶方阵![]() 可逆充分必要条件是
可逆充分必要条件是![]() 的行列式
的行列式![]() =( ),可逆时
=( ),可逆时![]() ( )
( )
3.矩阵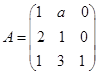 不是可逆矩阵,则
不是可逆矩阵,则![]() 的值等于( )。
的值等于( )。
4. 设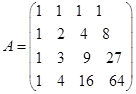 ,则
,则![]() ( )
( )
5. ![]() 阶方阵
阶方阵![]() ,
,![]() 是
是![]() 的伴随矩阵,则
的伴随矩阵,则![]() ( )。
( )。
二.选择题
1.下列关于矩阵乘法交换性的结论中错误的是( )。
A.若![]() 是可逆矩阵,则
是可逆矩阵,则![]() 与
与![]() 可交换;
可交换;
B.可逆矩阵必与初等矩阵可交换;
C. 任一![]() 阶矩阵与
阶矩阵与![]() 的乘法可交换,这里
的乘法可交换,这里![]() 为常数;
为常数;
D. 初等矩阵与初等矩阵的乘法未必可交换。
2.若![]() 是
是![]() 阶可逆矩阵,经过若干次初等变换后,其行列式的值( )。
阶可逆矩阵,经过若干次初等变换后,其行列式的值( )。
A.保持不变; B. 保持不为零;
C. 可以变为任何值; D. 保持相同的符号。
3.设![]() 为方阵,分块对角矩阵
为方阵,分块对角矩阵![]() ,则
,则![]() ( )。
( )。
A. 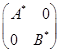 ; B.
; B. 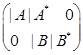 ;
;
C. 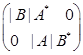 ; D.
; D. 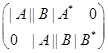 。
。
4. 设![]() 均为
均为![]() 阶可逆矩阵,则
阶可逆矩阵,则![]() 为( )。
为( )。
A.![]() ; B.
; B. ![]() ;
;
C. ![]() ; D.
; D. ![]() 。
。
5.设![]() 是
是![]() 矩阵,
矩阵,![]() 是
是![]() 阶可逆矩阵,
阶可逆矩阵,![]() ,若
,若![]() ,则( )。
,则( )。
A.![]() ; B.
; B. ![]() ;
;
C. ![]() ; D.
; D. ![]() 与
与![]() 的关系依
的关系依![]() 而定。
而定。
三.计算题
1. 设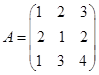 ,求
,求![]() 。
。
2.设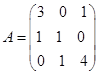 ,且满足
,且满足![]() ,求矩阵
,求矩阵![]() 。
。
3,设
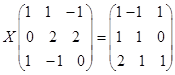 ,
,
求![]() 。
。
四.证明题
1. 如果![]() ,证明:
,证明:![]() 当且仅当
当且仅当![]() .
.
2. 矩阵![]() 称为反对称,如果
称为反对称,如果![]() . 证明:任一
. 证明:任一![]() 矩阵都可表为一对称阵与一反对称阵之和.
矩阵都可表为一对称阵与一反对称阵之和.
3. 设![]() ,
,![]() 为
为![]() 矩阵. 证明:如果
矩阵. 证明:如果![]() ,那么
,那么
秩![]()
![]() 秩
秩![]()
![]() .
.

