当前位置:课程学习>>第五章 矩阵>>拓展资源>>拓展学习
文本资源
学习指导
一、内容提要
1.基本概念
1)矩阵的乘法,矩阵的逆,伴随矩阵;
2)分块矩阵,初等矩阵,分块矩阵的初等变换,矩阵的等价。
2.基本结论
1)矩阵乘积的行列式性质;
2)矩阵秩的性质;
3)可逆矩阵存在的充分必要条件;
4)初等变换与初等矩阵之间的关系。
3.基本方法
1)伴随矩阵与初等变换两种方法求逆矩阵;
2)初等变换与子式两种方法求矩阵的秩;
3)分块矩阵的初等变换技巧。
4.需要说明的问题
本章重点是掌握矩阵的运算以及它们的运算规律。具体学习过程中,应注意以下几个方面的问题:
1. 由于矩阵运算和熟知的数的运算规律有些是相同的,但也有许多不同之处,这些不同之处正是易犯错误的地方。学习过程中应该特别在意。
2. 伴随矩阵![]() 是为计算逆矩阵而引人的,但在具体求逆矩阵时,只对低级矩阵(特别是2级矩阵)采用伴随矩阵法进行计算,对2级以上矩阵利用初等变换法求逆矩阵更方便。在涉及伴随矩阵的有关计算及证明时,往往利用伴随矩阵的基本公式
是为计算逆矩阵而引人的,但在具体求逆矩阵时,只对低级矩阵(特别是2级矩阵)采用伴随矩阵法进行计算,对2级以上矩阵利用初等变换法求逆矩阵更方便。在涉及伴随矩阵的有关计算及证明时,往往利用伴随矩阵的基本公式![]() ,来推证及化简。注意学会应用公式
,来推证及化简。注意学会应用公式![]() 证明相关问题。
证明相关问题。
3. 利用初等矩阵及分块初等矩阵可以将对矩阵的初等变换和分块矩阵的分块初等变换转化成矩阵的乘法运算,对于解决一些涉及矩阵理论和计算题很有用,但推证过程有一定技巧,需要不断训练总结。
4. 有关矩阵的秩的等式或不等式的证明,常常和向量组的秩,线性方程组的解等相联系,推证有一定的难度。熟记关于矩阵的秩的一些结论,对有关问题的论证会有很大的帮助。
二、精选例题解析
例1已知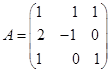 ,
,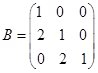 ,
,
求(1)![]()
![]() 。
。
解 (1)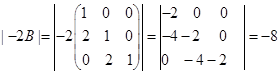 .
.
注意下面的计算是错误的
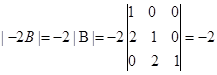
(2)
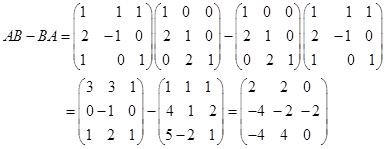
例2 设![]() 都是
都是![]() 阶方阵。试问下列等式是否成立?若成立,说明理由;若不成立,举例说明。
阶方阵。试问下列等式是否成立?若成立,说明理由;若不成立,举例说明。
(1)![]() ;
;
(2) ![]() ,则
,则![]()
(3)![]()
(4)![]() ,则
,则![]() 或
或![]()
(5)![]()
(6)![]()
(7)![]() 则
则![]()
解 矩阵运算中,由于矩阵的乘法不满足交换律,所以(1),(3)都是错误的。(1)应改为![]() 。
。
(3)![]() 。
。
又矩阵的乘法运算中,消去律不成立。例如
![]() ,
,
则![]() 但
但![]() ,所以(2)错误。
,所以(2)错误。
(4)因为![]() ,即
,即![]() ,不能推出
,不能推出![]() 或
或![]() 。即不能得
。即不能得![]() 或
或![]() 。例如
。例如![]() 有
有![]() 但
但![]() 且
且![]() ,所以结论错误。
,所以结论错误。
(5)错误。因为当![]() 为偶数时,
为偶数时,![]() ,
,
例如![]() 则
则![]() 。所以结论错误。
。所以结论错误。
(6)错误。例如![]() ,则
,则![]() 而
而![]() ,所以
,所以![]() ,所以
,所以![]() 。
。
(7)错误。例如![]() ,但
,但![]() 。
。
例 3设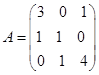 ,且满足
,且满足![]() ,求矩阵
,求矩阵![]() 。
。
解 由![]() ,有
,有![]() ,而
,而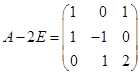 ,且
,且![]() ,所以
,所以![]() 可逆,有逆阵存在。于是
可逆,有逆阵存在。于是
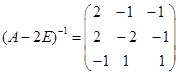
所以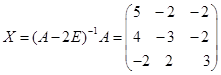 。
。
例4求矩阵的逆阵
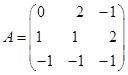 。
。
解 用伴随矩阵与初等行变换求逆阵。
(1)伴随矩阵法
![]() 所以
所以![]() 可逆。
可逆。![]() 。
。
因为
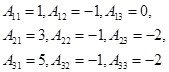
所以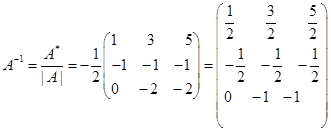 。
。
(2)初等行变换法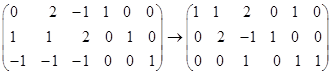
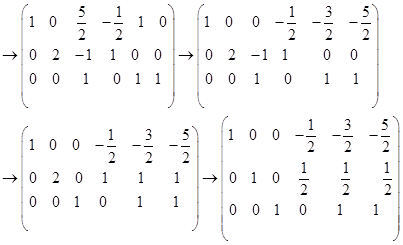 所以
所以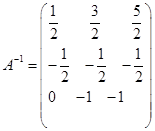 。
。
例5 已知![]() 阶方阵
阶方阵![]() ,满足
,满足![]() ,证明
,证明![]() 可逆,并求
可逆,并求![]() 。
。
证明 因为![]() ,得
,得![]() ,
,
两边加![]() ,得
,得![]() ,
,
整理得![]()
所以![]() 可逆,且
可逆,且![]() 。
。
例6 证明:任一![]() 阶方阵都可以表示为一个队称矩阵和反对称矩阵的和,且表示唯一。
阶方阵都可以表示为一个队称矩阵和反对称矩阵的和,且表示唯一。
证明 设![]() ,其中
,其中![]() 为对称矩阵,
为对称矩阵,![]() 为反对称矩阵,
为反对称矩阵,![]() 两边取转置,得
两边取转置,得
![]() ,
,
解矩阵方程组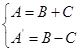 ,得
,得
![]() ,显然
,显然![]() ,
,![]() 为对称矩阵,
为对称矩阵,![]() ,
,![]() 为反对称矩阵。
为反对称矩阵。
再证唯一性:若另有![]() ,其中
,其中![]() ,
,
则![]() ,
,
于是有![]() ,
,
所以![]() ,即有
,即有![]() ,唯一性得证。
,唯一性得证。
例7 设![]() 都是
都是![]() 阶方阵,如果
阶方阵,如果![]() ,证明
,证明 ![]() 。
。
证明 设![]() ,即
,即![]() 是
是![]() 的列向量。由
的列向量。由![]() ,得
,得![]() 即
即![]() 是方程组
是方程组![]() 的解向量。
的解向量。
又方程组![]() 的解向量组的秩为
的解向量组的秩为![]() ,
,
所以有 ![]() ,
,
所以 ![]() 。
。
例8.设![]() 为
为![]() 阶方阵,且
阶方阵,且![]() ,证明
,证明
![]() 。
。
证明 因为![]() ,则
,则![]() 即
即![]() 由例7结论有
由例7结论有
![]() 。又因为
。又因为
![]()
所以![]() ,于是有
,于是有![]() 。
。


