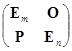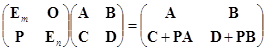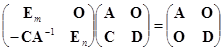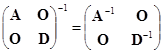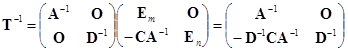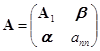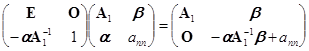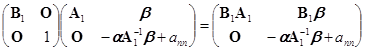当前位置:课程学习>>第五章 矩阵>>学习内容>>文本学习>>知识点七
知识点七:分块乘法的初等变换及应用举例
将分块乘法与初等变换结合就成为矩阵运算中极端重要的手段.现将某个单位矩阵如下进行分块:
对它进行两行(列)对换;某一行(列)左乘(右乘)一个矩阵![]() ;一行(列)加上另一行(列)的
;一行(列)加上另一行(列)的![]() 的倍数,就可得到如下类型的一些矩阵:
的倍数,就可得到如下类型的一些矩阵:
和初等矩阵与初等变换的关系一样,用这些矩阵左乘任一个分块矩阵
只要分块乘法能够进行,其结果就是对它进行相应的变换:
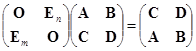 ,
, ![]()
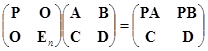 ,
, ![]()
同样,用它们右乘任一矩阵,进行分块乘法是也有相应的结果,我们不写了.
在![]() 中,适当的选择
中,适当的选择![]() ,可使
,可使![]() . 例如
. 例如![]() 可逆时,选
可逆时,选![]() ,则
,则![]() . 于是
. 于是![]() 的右端成为
的右端成为
![]() .
.
这种形状的矩阵在求行列式、逆矩阵和解决其它问题时是比较方便的,因此![]() 中的运算非常有用.
中的运算非常有用.
下面举些例子看看这些公式的应用.
例 ![]()
![]() ,
,![]() 可逆,求
可逆,求![]() .
.
由
及
易知
例 ![]()
![]() ,
,
设![]() 可逆,
可逆,![]() 可逆,试证
可逆,试证![]() 存在,并求
存在,并求![]() .
.
由
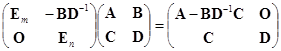 .
.
而右端仍可逆,故![]() 存在.
存在.
再由例![]() ,知
,知
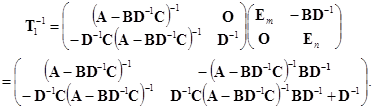
作
![]() .
. ![]()
设![]() ,
,![]() 为
为![]() 矩阵,作
矩阵,作
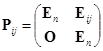 ,
,
![]() ,这里
,这里![]() 为
为![]() 矩阵,除了第
矩阵,除了第![]() 行第
行第![]() 列元素为
列元素为![]() 外,其他元素皆为零. 则由初等矩阵与初等变换的关系,易知右端为
外,其他元素皆为零. 则由初等矩阵与初等变换的关系,易知右端为
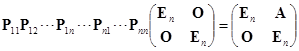 .
.
又由![]() 所对应的初等变换是某行加上另外一行的倍数,它不改变行列式的值,故
所对应的初等变换是某行加上另外一行的倍数,它不改变行列式的值,故
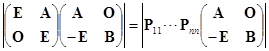
![]() .(第二章§
.(第二章§![]() 例
例![]() )
)
但![]() 的右端可经
的右端可经![]() 个两列对换变成
个两列对换变成
![]() ,
,
故
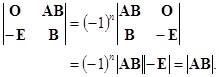
这就证明了
![]() .
.
例 ![]() 设
设 ![]() ,且
,且
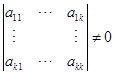 ,
,![]() ,
,
则有下三角形矩阵![]() 使
使
![]() 上三角形矩阵.
上三角形矩阵.
证明 对![]() 作归纳法. 当
作归纳法. 当![]() 时,一阶矩阵既是上三角形又是下三角形. 故命题自然成立.
时,一阶矩阵既是上三角形又是下三角形. 故命题自然成立.
设对![]() 命题为真,我们来看
命题为真,我们来看
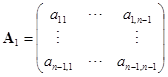 ,
,
它仍满足命题中所设的条件. 由归纳法假设,有下三角形矩阵![]() 满足
满足
![]() =上三角形矩阵.
=上三角形矩阵.
对![]() 作如下分块,
作如下分块,
则
在作
这时矩阵已成为上三角形了. 将两次乘法结合起来就得到:
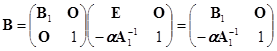 .
.
此即所要的下三角矩阵.
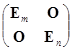
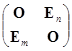
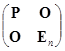
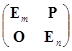 ,
,