一．填空题（每空4分，共20分）

1.已知向量 ，则 与 的夹角为   。

2.曲线方程为 ，设 ，则参数方程为

3.直线与直线的位置关系是平行。

4. 一直线通过点 ，方向角为 ，它的方程为

5.单叶双曲面的两族直母线方程为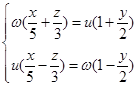与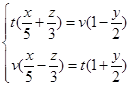

二．选择题（每题4分，共20分）

1.设三个向量 满足 ，则 =（     C    )

A.       B.     C.    D.

2.混合积（   C     )

A.     B.    C.   D.

3.通过点 ，且与平面 垂直的直线方程为（   C   )

A.              B.

C.             D.

4.通过点 ，且与直线垂直的平面方程为（    B     )

A.               B.

C.              D.

5.下列曲线中是双曲型的是（    B     )

A. 

B.

C.

D.

三．计算与证明题（共60分）

1.（10分）在空间直角坐标系下，求通过点 且垂直于直线 的平面方程。

解：已知直线的方向向量为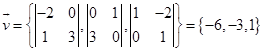 

因为直线方向既是所求平面的法向量，所以所求平面为为：，

即 

2.（20分） 在空间直角坐标系下，已知两直线，

（1）判定这两条直线的位置关系；

(2）若相交，求过 的交点，并且求出与它们都垂直的直线方程；若异面，求这两条直线间距离和公垂线方程。

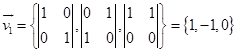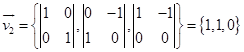解：（1）因为直线方向向量为，通过点  ；直线方向向量为，通过点 。

判别式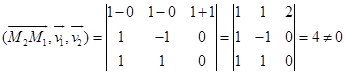 

 

所以直线是两条异面直线。

(2）的公垂线方向向量是 

因为所求直线与都垂直，所以方向向量为

所以间的距离是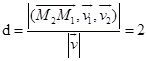

公垂线方程为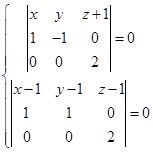

即： 

3.（15分）求顶点为（1，2，4），轴与平面 垂直，且经过点（1，2，1）的圆锥面方程。

解：设 是准线上的任意点，那么过 的母线为： 

且有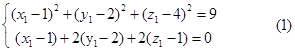

设

那么

将（2）代入（1），消去参数得所求圆锥面方程为：

 。

4.（15分）判断二次曲线的类型,求其简化方程及相应的坐标变换公式。

解:

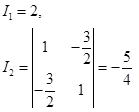，        系数矩阵：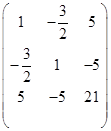

因为, 所以为双曲型曲线。

其特征方程为

特征根

非渐近主方向

轴:  ，即

轴:  ，即

取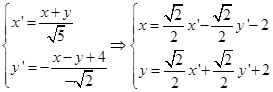（为相应坐标变换公式）

 

将其代入原曲线方程得简化方程为，即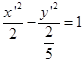。