当前位置:课程学习>>第一章>>本章练习>>参考答案
参考答案
1证明:因为 ![]() ,故
,故![]() ,所以
,所以![]() 三点共线。
三点共线。
2.证明:设![]() ,故
,故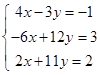 ,解得
,解得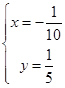
故![]() 共面。
共面。
3.解:![]() ,因为它们的坐标不对应成比例,所以这三个点不共线。
,因为它们的坐标不对应成比例,所以这三个点不共线。
4.解:因为
![]()
故![]() 。
。
5.解:利用两个向量的内积公式及向量的内积运算律,得(1)5;(2)5;(3)![]() 。
。
6.解:设![]() ,利用两个向量的内积公式得
,利用两个向量的内积公式得![]() ,利用两个向量的外积模长公式及向量的外积运算律,得(1)4;(2)36。
,利用两个向量的外积模长公式及向量的外积运算律,得(1)4;(2)36。
7.解:由于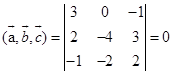 ,故
,故![]() 共面。
共面。
8.证明:利用三个向量的双重向量积公式证明。