参考答案

---

1.解：设

 因为 ，所以点在二次曲线上。

而

所以

因此点为二次曲线的正常点，从而切线方程为：

即 

 

2.解：曲线的中心满足： ，解得中心为： 

曲线的渐近方向满足： ，解得渐近方向为： 

所以所求的渐近线方程为：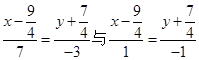

即： 。

3.解：所求的弦就是过点的直径的共轭弦，

经过点的直径，即为 与两点间的连线，其方程为： ，

所以直径的方向为： ，设与其共轭的方向为 ，利用关系式 

得

故被点 平分的弦的方程为： 

即 。

4.解：设所求的二次曲线方程为:

  

因为它通过点 与 

所以有 

与 

两共轭直径 与 的交点 即为二次曲线的中心，因此有：

 

 

又因为两直径的方向为一对共轭方向，所以有 

由（1），（2），（3），（4），（5）解得： 

故所求曲线方程为：  。

5.解：法一：

因为 ，所以曲线为中心曲线，解中心方程组： 

得曲线的中心为 ，取曲线的中心为新坐标系的原点，做移轴 

原方程变为： 

再进行转轴消去交叉项，取旋转角 ，满足： 

所以 

所以 

取 

得转轴公式为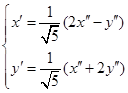 ，代入（1）并化简得 

相对应的坐标变换公式为 。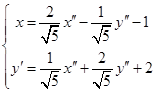

法二：

因为 

所以特征方程为： 

解得两特征根为： 

由确定的主方向为，

由确定的主方向为

所以两主直径方程分别为 

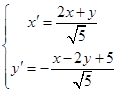
取主直径 为 轴， 为 轴，作坐标变换 ，解得

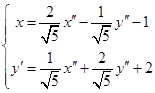，代入原曲线方程，经整理得曲线的简化方程为。

6解：（1）系数矩阵为 ， ，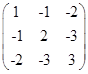 

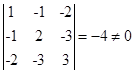
故曲线是中心型曲线中的椭圆。

(2) 系数矩阵为 ， ，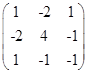 

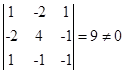
故曲线是非中心型曲线中的抛物线。

(3) 系数矩阵为 ， ，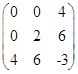 

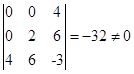
故曲线是非中心型曲线中的抛物线。

 

(4) 系数矩阵为 ， ， 

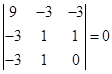
故曲线是非中心型曲线中的线心曲线。