1．不变量与半不变量

二次曲线在任意给定的直角坐标系中的方程为

         （1）

设在直角坐标变换(5.6-3)

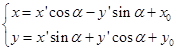
下，曲线方程（1）的左端变为

那么多项式也是二元二次多项式，它的每一个系数都可以用多项式的系数和坐标变换(5.6-3)的系数表出。

定义1  由的系数组成的一个非常数函数，如果经过直角变换(5.6-3)，变为时，有

那么这个函数叫做二次曲线（1）在直角坐标变换(5.6-3)下的不变量。如果这个函数的值，只是经过转轴变换不变，那么这个函数叫做二次曲线（1）在直角坐标变换下的半不变量。

定理1  二次曲线（1）在直角坐标变换下，是不变量，是一个半不变量。

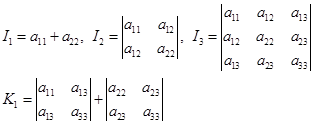
证  因为直角坐标变换(5.6-3)总可以分成移轴(5.6-1)与转轴(5.6-2)两步来完成，因此定理的证明。也就分成移轴与转轴两步来完成。

先证明在移轴(5.6-1)下，不变，而一般要改变。

根据知(5.6-6)，在移轴下，二次曲线（1）的二次项系数不变

所以

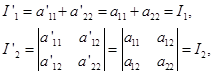
而

上面的第三个等式是由第三列减去第一列乘以，第二列乘以而得到的，第四个等式是由第三行减去第一行乘以，第二行乘以而得到的。

在移轴下一般是要改变的，例如，它的，而通过移轴(5.6-1)，变为

而这时

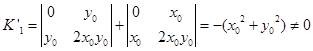
现在我们来证明转轴(5.6-2)下，与都不变。对于与只要考虑方程的二次项系数就够了，根据(5.6-7)，在转轴下有

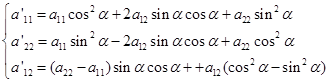      (2)

得用三角函数关系

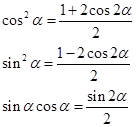
（2）可化为；

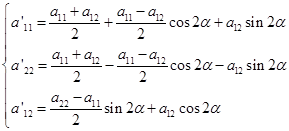
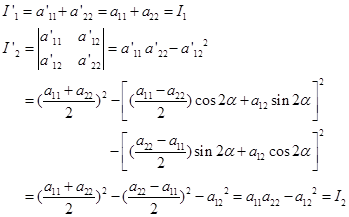
现在来证明在转轴下也不变。因为

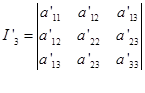
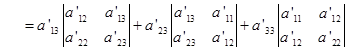
而在转轴下，刚才已证得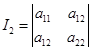不变。即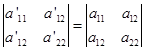，且在转轴下二次曲线方程的常数项不变。所以又有，因此

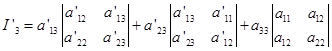
将(5.6-7)代入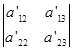，化简整理得

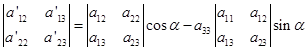
同理可得

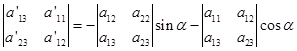
所以

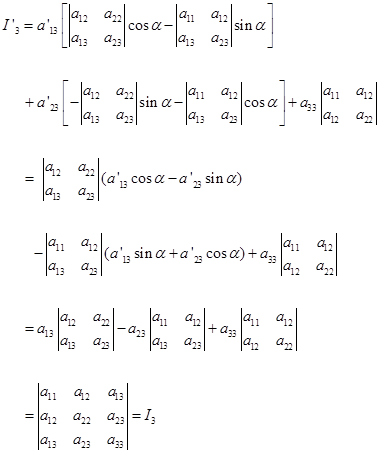
最后我们来证明在转轴下也是不变的，因为

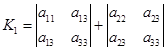
而与二次曲线（1）的常数项在转轴下都是不变的，又

所以

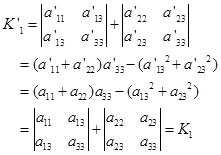
定理证毕。

定理2  当二次曲线（1）为线心曲线时，在直角坐标变换下是不变量。

证  首先证明当线心曲线的方程具有简化方程

（III）

对不变，因为是半不变量，所以只要证它在移轴下不变。

在移轴(5.1-1)下，（III）的左端变为

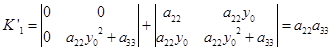
而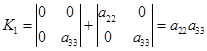   

则   

其次，如果经过移轴(5.6-1)变成（III），那么反过来（III）经过移轴就变成，所以当线心二次曲线通过移轴其方程能化成（III）时，那么不变。

现在设线心二次曲线经过任意的直角坐标变换变成，我们来证明。因为为线心二次曲线，因此总存在直角坐标变换把变成（III）的左端，因此反过来也一定可以通过直角坐标变换把（III）左端变成，再通过坐标变换把变成，也就是存在一个直角坐标变换把（III）的左端变成，变换的过程，如下图所示：

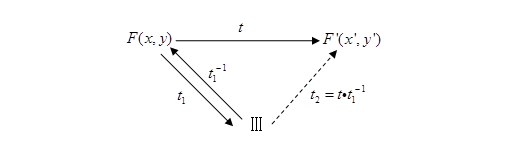
因此根据前面已证明的，当通过直角坐标变换把变成（III）的左端时不变，所以有

而通过直角坐标变换把（III）的左端变为时，又有

所以

定理证毕。

2．应用不变量化简二次曲线的方程

在定理5.6.1中已经指出，任何一个二次曲线的方程总可以化成三个简化方程(I)，(II)，(III)中的一个。在这里我们将应用二次曲线的三个不变量与一个半不变量来化简二次曲线的方程。这种方法可以不必求出具体的坐标变换公式，只要计算一下这些不变量与半不变量就可以决定二次曲线的简化方程。从而可以写出它的标准方程。现在我们仍然分中心曲线、无心曲线与线心曲线三种情况来讨论。

1）中心曲线    这时，它的简化方程为

(I)      

因此我们有      

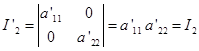
根据二次方程的根与系数的关系知道，与是特征方程

的两根，即分别是二次曲线的特征根。

其次又有

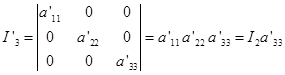
而                   

所以

这样我们就得到

定理3  如果二次曲线（1）是中心曲线，那么它的简化方程为

                        (5.7-1)

其中是二次曲线特征方程的两个根（方程中的撇号已略去）。

例1  求二次曲线的简化方程与标准方程。

解  因为

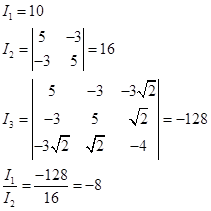
而特征方程的两根为

所以曲线的简化方程（略去撇号）为：

曲线的标准方程（略去撇号）为：

这是一个椭圆。

2）无心曲线  这时或，它的简化方程为

(II)      

因此我们有

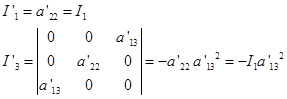
而            

所以

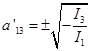
因此有

定理4  如果二次曲线（1）是无心曲线，那么它的简化方程为

                    (5.7-2)

这里的正负号可以任意选取（方程中的撇号已略去）。

例2  求二次曲线

的简化方程与标准方程

解

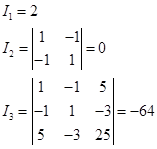
曲线的简化方程（略去撇号）为

  或  

它的标准方程（略去撇号）为

  或 

曲线为一条抛物线。

3）线心曲线  这时或，它的简化方程为

(III)     

因此我们有        

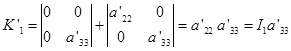
而             

所以

因此有

定理5  如果二次曲线（1）是线心曲线，那么它的简化方程为（方程中的撇号已略去）

                          (5.7-3)

从(5.7-1), (5.7-2), (5.7-3)我们又可以得到

定理6 如果给出了二次曲线（1），那么用它的不变量与半不变量来判断已知曲线为何种曲线的条件是：

（1）椭圆：         

（2）虚椭圆： 

（3）点（或称一对交于实点的共轭虚直线）：

（4）双曲线；  

（5）一对相交直线： 

（6）抛物线： 

（7）一对平行直线    

（8）一对平行的虚直线： 

（9）一对重合的直线   

这个定理的证明与定理5.6.2十分类似，它的证明留给读者。

推论  二次曲线（1）表示两条直线（实的或虚的，不同的或重合的）的充要条件为。