第一章 热力学第一定律
 知识点八:化学反应焓变的计算
知识点八:化学反应焓变的计算
等温、等压下,化学反应的焓变△rHm等于产物焓的总和与反应物焓的总和之差
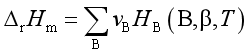
若能知道反应系统中各个化合物(或元素)焓的绝对值,则只要把焓的绝对量代入上式,就可计算出反应的焓变。由于焓的绝对量无法实验测定,人们通常采用一种相对标准求出焓的相对量,可用来计算反应的△rHm。
一、标准摩尔生成焓
等温、等压下,化学反应的焓变△rHm等于产物焓的总和与反应物焓的总和之差
 (41)
(41) 若能知道反应系统中各个化合物(或元素)焓的绝对值,则只要把焓的绝对量代入式(41),就可计算出反应的焓变。由于焓的绝对量无法实验测定,人们通常采用一种相对标准求出焓的相对量,可用来计算反应的△rHm。
人们规定:在指定温度下,由稳定的单质生成化学计量数![]() 的产物B时的标准摩尔反应焓变, 称为物质B的标准摩尔生成焓,并用符号
的产物B时的标准摩尔反应焓变, 称为物质B的标准摩尔生成焓,并用符号 (B,β,T)表示,其中β表示物质B的聚集状态。使用时注意:习惯上经常使用的是25℃时的标准摩尔生成焓
(B,β,T)表示,其中β表示物质B的聚集状态。使用时注意:习惯上经常使用的是25℃时的标准摩尔生成焓 (B,β,298.15K)。稳定单质是指定条件下最稳定的状态,如碳的稳定单质是石墨,Br2的稳定单质是液态溴等。
(B,β,298.15K)。稳定单质是指定条件下最稳定的状态,如碳的稳定单质是石墨,Br2的稳定单质是液态溴等。
一些物质的标准摩尔生成焓的数据可由实验测得,例如:
C(石墨)+O2(g) → CO2(g) ,  (CO2, g, 298.15K)=-393.5 kJ·mol-1
(CO2, g, 298.15K)=-393.5 kJ·mol-1
H2(g) +![]() O2(g) → H2O(l),
O2(g) → H2O(l),  (H2O, l, 298.15K)=-285.8 kJ·mol-1
(H2O, l, 298.15K)=-285.8 kJ·mol-1
而更多化合物并不是由稳定单质直接生成的,例如C2H5OH(l)不能通过下述反应制备:
因此,就不能由实验直接测定C2H5OH(l)的标准摩尔生成焓,可以通过其他途径,借助盖斯定律来计算得到。
例13 已知25℃时, C2H5OH (l)+3 O2 (g) →2 CO2 (g) + 3 H2O (l)的标准摩尔反应焓变为-1367kJ·mol-1。试根据CO2(g)和H2O(l)的 ,计算25℃时C2H5OH(l)的标准摩尔生成焓。
,计算25℃时C2H5OH(l)的标准摩尔生成焓。
解 设计反应途径,并写出各热化学方程式:
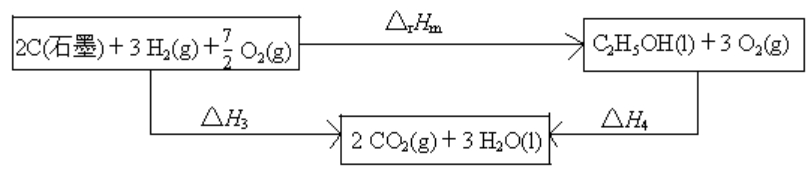
① C(石墨) + O2(g) → CO2(g), 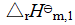 =-393.5kJ·mol-1
=-393.5kJ·mol-1
② H2(g) +![]() O2(g) → H2O(l),
O2(g) → H2O(l), 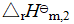 =-285.8kJ·mol-1
=-285.8kJ·mol-1
由式①和式②运算得式③
③ 2C(石墨) +3H2(g) +![]() O2(g) → 2CO2(g) + 3 H2O(l)
O2(g) → 2CO2(g) + 3 H2O(l)
所以, 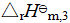 =2
=2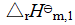 +3
+3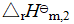 =-1644.3 kJ·mol-1
=-1644.3 kJ·mol-1
④ C2H5OH(l) + 3 O2(g) →2CO2(g) + 3 H2O(l), 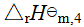 =-1367 kJ·mol-1
=-1367 kJ·mol-1
式③-式④,得
所以,  =
=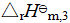 -
-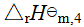
={-1644.4+1367}kJ·mol-1=-277.4 kJ·mol-1
即  (C2H5OH, l, 298.15K)=-277.4 kJ·mol-1
(C2H5OH, l, 298.15K)=-277.4 kJ·mol-1
化学反应的标准摩尔反应焓变可以由参加反应物质的标准摩尔生成焓求得。
例14 求25℃、100kPa下,Al2O3(s) + 3SO3(g) → Al2(SO4)3(s) 的标准摩尔反应焓变。已知Al2O3(s)、SO3(g)和Al2(SO4)3(s)的标准摩尔生成焓 分别为-1669.79 kJ·mol-1、-395.18 kJ·mol-1和-3434.98 kJ·mol-1。
分别为-1669.79 kJ·mol-1、-395.18 kJ·mol-1和-3434.98 kJ·mol-1。
解 根据题意,可以设计反应途径,并由此写出热化学方程式:
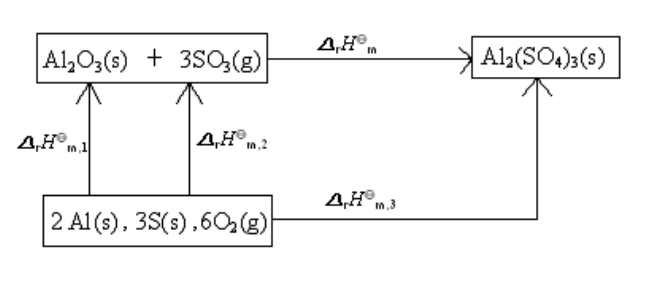
①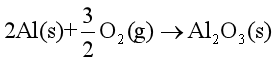 ,
, 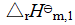 = -1669.79 kJ·mol-1
= -1669.79 kJ·mol-1
②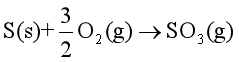 ,
, 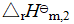 = -395.18kJ·mol-1
= -395.18kJ·mol-1
③![]() ,
, 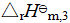 = -3434.98 kJ·mol-1
= -3434.98 kJ·mol-1
按盖斯定律可得,
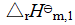 +3
+3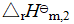 +
+ =
=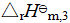
所以,  =
= 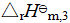 -(
-(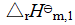 +3
+3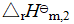 )
)![]()
从上例可看出,一定温度下,化学反应的标准摩尔反应焓变 ,等于同温度下产物的标准摩尔生成焓之和减去反应物的标准摩尔生成焓之和,或用反应前后各物质的标准摩尔生成焓与其化学计量数乘积之和表示。即
,等于同温度下产物的标准摩尔生成焓之和减去反应物的标准摩尔生成焓之和,或用反应前后各物质的标准摩尔生成焓与其化学计量数乘积之和表示。即
 =
= 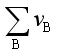
 (B,β,T) (42)
(B,β,T) (42) 二、标准摩尔燃烧焓
一定温度下,化学计量数![]() 的物质B与氧气进行完全燃烧反应的标准摩尔反应焓变,称为物质B的标准摩尔燃烧焓。用
的物质B与氧气进行完全燃烧反应的标准摩尔反应焓变,称为物质B的标准摩尔燃烧焓。用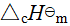 (B,β,T)表示,通常使用的是25 ℃时的数据。所谓完全燃烧是指产物处于稳定的聚集状态,规定燃烧物中的C转变为CO2(g)、H转变为H2O(l)、S转变为SO2(g)、N转变为N2(g)等等。
(B,β,T)表示,通常使用的是25 ℃时的数据。所谓完全燃烧是指产物处于稳定的聚集状态,规定燃烧物中的C转变为CO2(g)、H转变为H2O(l)、S转变为SO2(g)、N转变为N2(g)等等。
例如,298.15K,100 kPa时
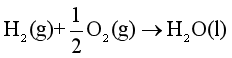 ,
, 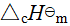 (H2,g,298.15K)= –285.83kJ·mol-1
(H2,g,298.15K)= –285.83kJ·mol-1 根据盖斯定律,可得由物质B的标准摩尔燃烧焓计算反应的标准摩尔反应焓变的公式如下:
 = -
= -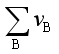
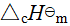 (B,β,T) (43)
(B,β,T) (43) 上式表示,任一反应的标准摩尔反应焓变 等于反应物的标准燃烧焓之和减去产物的标准燃烧焓之和。
等于反应物的标准燃烧焓之和减去产物的标准燃烧焓之和。
例15 已知25℃时,丙烯腈CH2CHCN(l)、C(石墨)和H2(g)的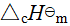 分别为 –1759.5、–393.5、–285.9kJ·mol-1;在相同温度下,丙烯腈的摩尔蒸发焓为32.84 kJ·mol-1,HCN(g)和C2H2(g)的
分别为 –1759.5、–393.5、–285.9kJ·mol-1;在相同温度下,丙烯腈的摩尔蒸发焓为32.84 kJ·mol-1,HCN(g)和C2H2(g)的 分别为135.1 kJ·mol-1和226.7kJ·mol-1。求25℃、标准状态下,反应HCN(g)+ C2H2(g) → CH2CHCN(g)的
分别为135.1 kJ·mol-1和226.7kJ·mol-1。求25℃、标准状态下,反应HCN(g)+ C2H2(g) → CH2CHCN(g)的 。
。
解 需先求HCN(g)和C2H2(g)的摩尔燃烧焓:
①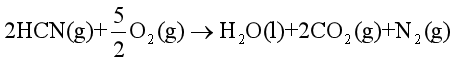
②
由燃烧焓和生成焓的定义可知:
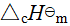 ( H2,g)=
( H2,g)= (H2O,l),
(H2O,l), 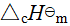 (石墨)=
(石墨)= (CO2, g),
(CO2, g),因此,由相关物质标准摩尔生成焓的数据,可求得式①、式②反应的标准摩尔反应焓变,实质上它们分别是HCN(g)和C2H2(g)的标准摩尔燃烧焓。
由反应式①求得
 = {-285.9}+ 2×(-393.5) -2×135.1} kJ·mol-1
= {-285.9}+ 2×(-393.5) -2×135.1} kJ·mol-1 = -1343.1 kJ·mol-1
所以,HCN(g)的标准摩尔燃烧焓
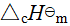 (HCN,g)=
(HCN,g)=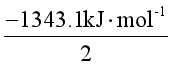 = -671.5 kJ·mol-1
= -671.5 kJ·mol-1 同样方法,可计算式②的标准摩尔反应焓变
 = {2×(-393.5) + (-285.9) - 226.7} kJ·mol-1
= {2×(-393.5) + (-285.9) - 226.7} kJ·mol-1
= -1299.6 kJ·mol-1
丙烯腈CH2CHCN(g)的标准摩尔燃烧焓为
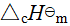 (CH2CHCN,g) =
(CH2CHCN,g) = 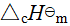 (CH2CHCN,l)-
(CH2CHCN,l)-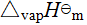 (CH2CHCN,l)
(CH2CHCN,l)
= -1759.5 kJ·mol-1 -32.84 kJ·mol-1
= -1792.34 kJ·mol-1
所以,HCN(g)+ C2H2(g) → CH2CHCN(g)的标准摩尔反应焓变
 =
= 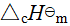 (HCN, g) +
(HCN, g) +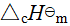 (C2H2, g) -
(C2H2, g) -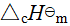 (CH2CHCN, g)
(CH2CHCN, g)
= {-671.5 + (-1299.6) -(-1792.34)} kJ·mol-1
= -178.76 kJ·mol-1
三、离子的标准摩尔生成焓
对于有离子参加的反应,若能知道离子的摩尔生成焓,则同样可以按式(43)计算该反应的摩尔焓变,只是在式中应用离子的摩尔生成焓数据去代替物质的摩尔生成焓数据。
所谓离子的摩尔生成焓是指从稳定单质生成无限稀释水溶液中该离子的摩尔焓变。若在298.15K以及各物质均处于标准状态时,则此焓变为离子标准摩尔生成焓,以 (B, aq,)表示。例如298.15K时,反应
(B, aq,)表示。例如298.15K时,反应
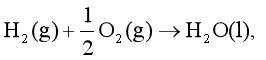
 = -285.8kJ·mol-1
= -285.8kJ·mol-1
H2O(l) → H+(∞,aq) + OH-(∞,aq),  = 55.84kJ·mol-1
= 55.84kJ·mol-1
两式相加,得
H2(g)+![]() O2(g) →H+(∞,aq) + OH-(∞,aq),
O2(g) →H+(∞,aq) + OH-(∞,aq),  (∞,aq)= -229.96 kJ·mol-1
(∞,aq)= -229.96 kJ·mol-1
所得结果为H+和OH-离子标准摩尔生成焓之和。可见,不能通过实验测定或设计辅助反应方程计算,求得单独一种离子的标准摩尔生成焓。若人为规定某种离子的标准摩尔生成焓为零作为一种基准,由此可以得到其他离子的标准摩尔生成焓,并可用他们来计算有离子参与反应的标准摩尔反应焓。通常规定298.15K、标准压力下,H+离子的 (H+,∞,aq)=0,显然,由上述结果,可求得OH-离子的
(H+,∞,aq)=0,显然,由上述结果,可求得OH-离子的 (OH-1,∞,aq) = -229.96 kJ·mol-1。
(OH-1,∞,aq) = -229.96 kJ·mol-1。
以H+和OH-的标准摩尔生成焓为基础,可求得其他离子的标准摩尔生成焓。例如,已知HCl(g)的标准摩尔生成焓和溶解焓分别为:
![]() H2(g) +
H2(g) + ![]() Cl2(g) → HCl(g),
Cl2(g) → HCl(g),  = -92.30 kJ·mol-1
= -92.30 kJ·mol-1
HCl(g) → H+(∞,aq) + Cl-(∞,aq), 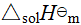 =-75.14 kJ·mol-1
=-75.14 kJ·mol-1
则  (H+,∞,aq)) +
(H+,∞,aq)) +  (Cl-1,∞,aq) = -167.44 kJ·mol-1
(Cl-1,∞,aq) = -167.44 kJ·mol-1
因为规定:  (H+,∞,aq) = 0
(H+,∞,aq) = 0
所以,  (Cl-1,∞,aq) = -167.44 kJ·mol-1
(Cl-1,∞,aq) = -167.44 kJ·mol-1
例1.16 溶液中有1mol Ca2+,其浓度很稀,25℃时通入过量CO2(g)后产生CaCO3沉淀,求沉淀反应的标准摩尔焓变。
解:设为无限稀释的溶液,发生下列反应:
Ca2+(∞,aq) + CO2(g)+H2O(l) → CaCO3(s) + 2H+(∞,aq)
 =[
=[ (CaCO3,s) + 2
(CaCO3,s) + 2 (H+,∞,aq)]
(H+,∞,aq)]
﹣[ (Ca2+,∞,aq) +
(Ca2+,∞,aq) +  (CO2,g)+
(CO2,g)+  (H2O,l)]
(H2O,l)]
={1206.87 + 0}kJ·mol-1-{-542.96-393.51-285.84} kJ·mol-1
= 15.44 kJ·mol-1
四、由键能估算反应焓变
1.键能
一切化学反应都可归结为原子、分子或原子团的重新排列组合,反应就是反应系统中的旧化学键断裂和新化学键形成的过程,能量变化是这种过程的必然结果之一,也是反应焓变的由来。若已知化合物的结构以及分子中各原子间的化学键能,则根据反应过程中化学键断裂和形成的情况就能算出反应焓变。但是,人们对物质微观结构的认识还有待于不断深化,实验技术仍落后于剖析微观世界的要求,现有的键能的数据还很不完善,而且不够准确。
热化学中所用键能与光谱数据所得的分解能在意义上有所不同。键能是指断裂气态化合物中某一具体化学键生成气态原子或原子团时所需的能量。根据光谱数据,断裂H2O(g)中的第一根O-H键和第二根O-H键所需的能量是不同的,例如
H2O(g) → H(g) + OH(g) ,  = 502.1 kJ·mol-1
= 502.1 kJ·mol-1
OH(g) →H(g) + O(g),  = 423.4 kJ·mol-1
= 423.4 kJ·mol-1
为便于应用,可以取H2O(g)中两根O-H的平均键能作为O-H的键能,即
![]() =
= ![]() = {
= {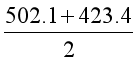 }kJ·mol-1 = 462.8 kJ·mol-1
}kJ·mol-1 = 462.8 kJ·mol-1
所以,键能不是实验的直接结果,只是在估算反应焓变时的一种数据。当选取作为平均值的基准物质不同时,键能的数据亦会出现差异。同一种键的键能,在不同情况下,也可能稍有出入。
对于双原子分子中的键,键解离能与键能是等同的,例如H2 ,O2等。
H2(g)→ 2H(g), ![]() =436.0 kJ·mol-1
=436.0 kJ·mol-1
O2(g)→ 2O(g), ![]() = 498.3 kJ·mol-1
= 498.3 kJ·mol-1
单纯用量热法不能求得断裂化合物中某一化学键所需的热量,键焓可利用一些光谱和量热数据的计算得的。例如计算C-H键焓的方法如下:
CH4(g) + 2O2(g) → CO2(g) + 2H2O(l), ![]() = -890.36 kJ·mol-1
= -890.36 kJ·mol-1
CO2(g) → C(石墨) + O2(g), ![]() = 393.51 kJ·mol-1
= 393.51 kJ·mol-1
2H2O(g) → 2H2 + O2(g), ![]() = 571.70 kJ·mol-1
= 571.70 kJ·mol-1
2H2 → 4H(g), ![]() = 877.00 kJ·mol-1
= 877.00 kJ·mol-1
C(石墨) → C(g), ![]() = 716.68 kJ·mol-1
= 716.68 kJ·mol-1
将上述五式相加,得
CH4(g) → C(g) + 4H(g), ![]() = 1668.53 kJ·mol-1
= 1668.53 kJ·mol-1
所以,在298.15K,C-H的键能
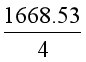 } kJ·mol-1 = 417.1 kJ·mol-1
} kJ·mol-1 = 417.1 kJ·mol-1 此数据与CH4(g)中C-H的键解离能(426.8kJ·mol-1)稍有差别。如果根据C2H6(g)的标准摩尔燃烧焓(-1559.9 kJ·mol-1)运用上述计算方法,可得如下反应的焓变:
C2H6(g) → 2C(g)+ 6H(g),  = 2827.8 kJ·mol-1
= 2827.8 kJ·mol-1
所以C-C的键能
表 3 一些键能数据(298.15K)
键 |
D/kJ·mol-1 |
键 |
D/kJ·mol-1 |
键 |
D / kJ·mol-1 |
|||
H-H |
436.0 |
C-H |
414 |
P-Cl |
326 |
|||
Li-Li |
105 |
N-H |
390 |
S-Cl |
-255 |
|||
N≡N |
944.7 |
O-H |
463 |
K-Cl |
423 |
|||
O-O |
139 |
F-H |
565 |
Ca-Cl |
368 |
|||
O=O |
498.3 |
Na-H |
197 |
As-Cl |
293 |
|||
F-F |
155 |
Si-H |
318 |
Se-Cl |
243 |
|||
Na-Na |
71 |
P-H |
322 |
Br-Cl |
217 |
|||
Si-Si |
222 |
S-H |
347 |
Rb-Cl |
427 |
|||
P-P |
200 |
Cl-H |
431.4 |
Ag-Cl |
301 |
|||
S-S |
225 |
K-H |
180 |
Sn-Cl |
318 |
|||
Cl-Cl |
242.3 |
Cu-H |
276 |
Sb-Cl |
310 |
|||
K-K |
49 |
As-H |
247 |
I-Cl |
209 |
|||
Ge-Ge |
188 |
Se-H |
276 |
Cs-Cl |
423 |
|||
As-As |
188 |
Br-H |
366 |
C-N |
292 |
|||
As≡As |
381 |
Rb-H |
163 |
C≡N |
890 |
|||
Se-Se |
209 |
Ag-H |
243 |
C-O |
350 |
|||
Se=Se |
272 |
C≡C |
835.1 |
C=O |
745 |
|||
Br-Br |
193 |
N-N |
163 |
C-S |
272 |
|||
Rb-Rb |
45.2 |
Te-H |
239 |
C=S |
536 |
|||
Sn-Sn |
163 |
I-H |
299 |
P-N |
577 |
|||
Sb-Sb |
121 |
Cs-H |
175.7 |
S=O |
498 |
|||
Sb≡Sb |
288.7 |
Li-H |
481 |
C≡O |
1046 |
|||
C-C |
344 |
C-Cl |
329 |
C-F |
328 |
|||
C=C |
610 |
N-Cl |
192 |
C-Br |
276 |
|||
Te-Te |
222 |
O-Cl |
218 |
C-I |
240 |
|||
I-I |
150.9 |
F-Cl |
253 |
C-Si |
290 |
|||
Cs-Cs |
43.5 |
Na-Cl |
410 |
N-O |
175 |
|||
Li-H |
243 |
Si-Cl |
380 |
|
|
|||
所得D(C-C)数据与表3稍有差异,原因如上述。
2.由键能估算反应的焓变
化合物中所有化学键的键能总和就是单位物质量的该气态化合物B全部离解为气态原子所需的能量。例如在298.15K时
CH4(g) → C(g) + 4H(g), ![]() = 4
= 4![]()
Se2Cl2(g) → 2Se(g) + 2Cl(g), ![]() =
=![]() + 2
+ 2![]()
C2H6(g) → 2C(g) + 6H(g), ![]() =
= ![]() + 6
+ 6![]()
根据键能数据可以估算化合物的摩尔生成焓。以Se2Cl2为例:
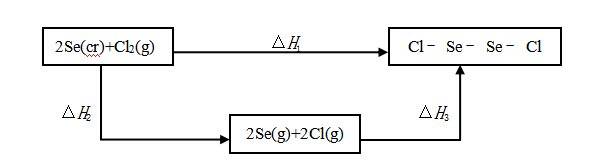
由物质的摩尔生成焓的定义可知,![]() =
= ![]() (Se2Cl2,g),
(Se2Cl2,g),![]() 为从稳定单质分子生成气态单原子的摩尔焓变,也就是各气态单原子的摩尔生成焓之和。气态单原子的摩尔生成焓也称为稳定单质分子的摩尔原子化焓。查得
为从稳定单质分子生成气态单原子的摩尔焓变,也就是各气态单原子的摩尔生成焓之和。气态单原子的摩尔生成焓也称为稳定单质分子的摩尔原子化焓。查得 (Se,g)为202.38 kJ·mol-1,
(Se,g)为202.38 kJ·mol-1,  (Cl,g)为121.29 kJ·mol-1.。
(Cl,g)为121.29 kJ·mol-1.。
所以, Δ![]() =
= ![]() =
=  (Se,g) +
(Se,g) +  (Cl,g)
(Cl,g)
= (2![]() 202.38+2
202.38+2![]() 121.29)kJ·mol-1
121.29)kJ·mol-1
= 647.34 kJ·mol-1
=-{209+2
由上例可知,由键能可估算化合物的摩尔生成焓。上例的特点是假设这样一个过程,即将稳定单分子拆散生成气态原子,然后再将气态原子组合成这个化合物的各种键。若化合物中含有许多种原子和许多种键,其中![]() 是B种原子的数目,
是B种原子的数目,![]() 是j种键的数目,其键能为
是j种键的数目,其键能为![]() ,该化合物的摩尔生成焓为
,该化合物的摩尔生成焓为
 =
= 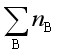
 (原子B,g) -
(原子B,g) - 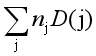
例17 根据键能数据和气态单原子的摩尔生成焓的数据,估算C2H50H(g)在298.15K时的摩尔生成焓。
解
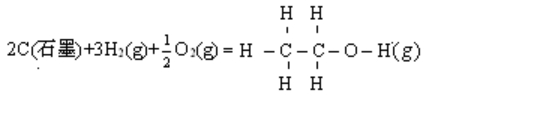
 (C2H5OH, g) = 2
(C2H5OH, g) = 2 (C, g) + 6
(C, g) + 6 (H, g) +
(H, g) + (O, g)
(O, g) 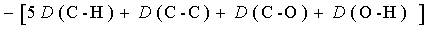
= {2×718.38 + 6×217.94 + 247.52} kJ·mol-1
-{5×414 + 344 + 350 + 463}kJ·mol-1
= -235 kJ·mol-1
与实验结果-235.4 kJ·mol-1基本相符。
必须指出,键能是一些键解离能的平均值,有些键能是由另一些键能计算而得,所以用键能计算化合物的摩尔生成焓以及反应焓变只是一种近似的方法。
五、反应焓变与温度的关系
反应的焓变与压力的关系很复杂,在通常条件下,压力对反应焓变的影响很小,甚至可以忽略。这里我们只讨论反应的焓变随温度变化的规律—基尔霍夫定律。
设等温、等压下的反应
反应的焓变应为产物的焓总和与反应物的焓总和的差值,即
在等压下,将式( 45)的两边同时对T微商,则
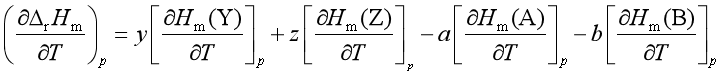
![]()
![]()
即 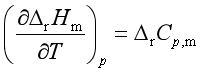 (45)
(45)
其中 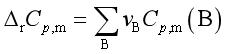 (46)
(46)
式(45)称为微分形式的基尔霍夫定律,表明在等压下,反应的焓变△rHm随温度T的变化率取决于反应系统的等压热容差△rCp,m。通常反应系统的![]() ≠0,所以反应的焓变随温度而变。
≠0,所以反应的焓变随温度而变。
若反应的焓变△rHm与压力p无关,则基尔霍夫定律的微分形式可表示为
若温度T1时的反应焓为△rHm(T1)、T2时反应焓为△rHm(T2), 式(48)的定积分形式为
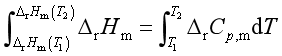 (48)
(48) 若设系统的等压热容差△rCp为与温度T无关的常量,定积分式(48),则
式(1.49)为基尔霍夫定律的定积分形式。此式表明,由温度T1时的反应焓△rHm(T1)、△rCp, m,可求得另一温度T2时的反应焓△rHm(T2)。习惯上我们常选择![]() 为298.15K,因为此温度、标态时反应的焓变
为298.15K,因为此温度、标态时反应的焓变 (T1)可从手册上提供的数据计算得到。
(T1)可从手册上提供的数据计算得到。
需注意的是,上述式(49)适用在所讨论的温度范围内反应系统中的物质均无相变发生的情形。若反应系统中有一种或几种物质发生相变化,需按照状态函数方法设计途径,由已知温度下的反应焓、有关物质在相变温度下的相变焓、定压摩尔热容,计算另一温度下的标准摩尔反应焓。
例18 已知下列物质的摩尔等压热容与温度的关系式分别为
![]() (H2,g)=
(H2,g)=![]() J·K-1·mol-1,
J·K-1·mol-1,
![]() (O2,g)=
(O2,g)= ![]() J·K-1·mol-1,
J·K-1·mol-1,
![]() (H2O,g)=
(H2O,g)=![]() J·K-1·mol-1,
J·K-1·mol-1,
以及反应H2 (g)+ O2(g) → 2 H2O(g)的标准摩尔反应焓 (298.15K)=-483.6kJ·mol-1,求1000K时的标准摩尔反应焓
(298.15K)=-483.6kJ·mol-1,求1000K时的标准摩尔反应焓 (1000K)。
(1000K)。
解 物质的摩尔等压热容与温度的关系采用Cp,m = a + bT + cT-2的形式。由已知数据可求得该反应的摩尔等压热容变化为
![]()
![]() J·K-1·mol-1
J·K-1·mol-1
根据基尔霍夫定律的定积分形式
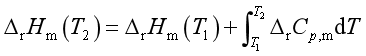
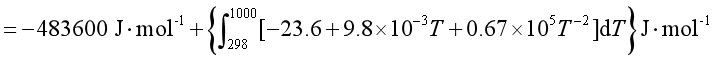
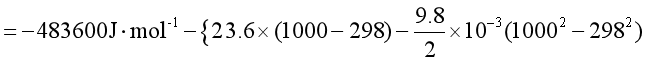
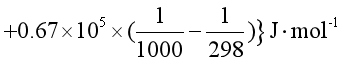
=-(483600 + 12260) J·mol-1=-498.86![]()
