一、单纯的pVT状态变化

系统发生简单状态变化时，若温度不变，则V和p都将改变，所以可根据基本公式之一式（40），或由对应系数关系式式（44）均可得

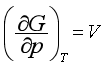
则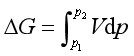                       

若知道V与p的函数关系，就能对上式积分求得ΔG。对于理想气体，可得

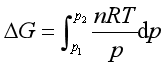
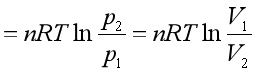（52）

对于凝聚系统，压力对体积影响不大，体积可视为常量，所以

ΔG＝V（p₂－p₁）（53）

等温的状态变化ΔG的计算，也可由G的定义式出发，因G＝H－TS，则
                   ΔG＝ΔH－Δ(TS)=

等温条件下

ΔG＝ΔH-TΔS

由ΔH和ΔS求得ΔG。例如理想气体，等温下ΔH＝0，所以

ΔG＝-TΔS＝－Q_R＝W_R

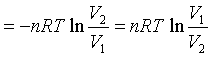
其结果与式（52）完全相同。

例7  300.2K时，1mol理想气体从10等温可逆膨胀到，求Q、W、ΔU、ΔH、ΔS、ΔA和ΔG。若由真空膨胀来完成同一变化，结果又将如何？

解  等温可逆膨胀
       
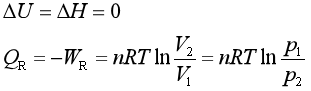
         =[8.314×300.2ln（10/1）] J =5747J
       
       

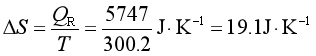
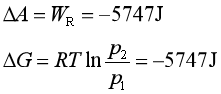
或由A和G的定义式可得，等温条件下

△A＝△G＝－T△S＝－Q_R＝W_R＝－5747J

若由真空膨胀完成同一变化，则W＝0，Q＝0。所有热力学函数的变化值只与系统的始、终态有关，因此它们的数值完全与可逆膨胀的结果相同。

二、相变化

1．可逆相变

可逆相变即是在相平衡温度、压力下进行的相变，此过程只作体积功。根据吉布斯自由能判据，等温等压、W′=0的可逆过程，ΔG=0。所以对于可逆相变，不必进行计算即可判定其ΔG=0。

例8 在373.2K和时，把1mol的水蒸气可逆压缩为液态水，计算Q、W、ΔU、ΔH、ΔS、ΔA和ΔG。已知该条件下水的蒸发热为40.69kJmol^-1。

解 W_R＝－p_eΔV＝－p（Vl－V_g）≈pV_g＝RT
      ＝8.314×373.2 Jmol^-1＝3103Jmol^-1
      Q_R=Q_p=Δ_vapH_m=－40.69×10³Jmol^-1
      ΔU=Q+W=(－40.69×10³+3.10³×10³)Jmol^-1＝－37.59×10³Jmol^-1
     
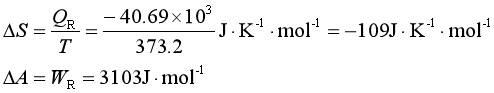
          （因为是等温等压可逆相变）

2．不可逆相变

不可逆相变即是在非相平衡温度、压力下进行的W′＝0的不可逆相变，该条件下的不可逆过程不可能通过相同条件的可逆过程来完成，与计算不可逆相变类似，也需设计一系列其他条件下的可逆过程完成此变化，其原则是不改变过程的温度（或压力），并由所设计的可逆过程来求得该变化的ΔG值。

例9 水在298.2K，下进行的相变：

H₂O（l，298.2K，）→H₂O（g，298.2K，）

计算该相变的ΔG，并判断变化能否自动进行。已知H₂O（l）在25℃时的饱和蒸气压为0.0313。

解 :这是不可逆相变过程，需设计过程求ΔG。在保持温度不变的条件下，将该相变与298.2K的可逆相变相联系，设计如下的可逆过程：

 

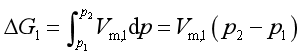    （因水的可压缩性甚微，V可作为常数）

（等温等压可逆相变）

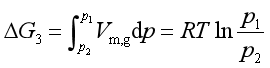
所以        ΔG＝ΔG₁+ΔG₂+ΔG₃
           ＝V_m,l（p₂-p₁）+RTlnp₁/p₂
           ＝[18.02×10-6×（0.0313-1）×10⁵+8.314×298.2ln0.0313] Jmol^-1
           ＝(-1.746+8591.3) Jmol^-1＝8590Jmol^-1
等温等压下ΔG＞0，说明变化不能自动进行。

通过以上计算可以看出，凝聚相（液相或固相）等温变压过程的ΔG₁要比气相同类过程的ΔG₃小得多，常常可以忽略不计。

三、化学变化

等温等压的化学反应

aA+bByY+zZ

除非反应已达平衡（Δ_rG_m＝0），则不论反应自发或非自发，过程均不可逆，因此需要设计可逆过程来计算反应的Δ_rG_m。

最简单的方法是将反应安排成可逆电池进行放电（自发反应）或充电（非自发反应），则

Δ_rG_m＝-zEF

但并非所有的反应都能安排成可逆电池，所以该方法不具有普遍性。

如果化学反应的Δ_rH_m和Δ_rS_m为已知时，便不必设计可逆过程，可直接由Δ_rH_m和Δ_rS_m计算Δ_rG_m，即

Δ_rG_m＝Δ_rH_m－TΔ_rS_m

化学反应的Δ_rG_m还有其他计算方法，如利用化学反应等温方程或利用物质的标准摩尔生成自由能等方法求Δ_rG_m。这些内容将在化学平衡一章中作详细论述。

例10 在298.2K和下，进行一化学反应，产生１mol气体,放热40.00×10³J。若通过可逆电池来完成反应，则吸热4.00×10³J。试计算反应的Δ_rH_m、Δ_rS_m、Δ_rA_m和Δ_rG_m。

解 反应在等温等压下不可逆进行时，

Q_p＝Δ_rH_m＝－40.00×10³J

＝－p_eΔ_rV_m≈－pV_g＝－nRT

  ＝（－1×8.314×298.2）J＝－2.48×10³J
则

Δ_rU_m＝Q_p+＝（－40.00×10³－2.48×10³）J＝－42.48×10³J

反应在可逆电池中进行时：

Q_R＝4.00×10³J

由可逆热Q_R可求得Δ_rS_m：

Δ_rS_m＝Q_R/T＝（4000÷298.2）JK^-1＝13.41JK^-1
Δ_rA_m＝Δ_rU_m－TΔ_rS_m＝（－42.48×10³－4.00×10³）J＝－46.48×10³J
Δ_rG_m＝Δ_rH_m－TΔ_rS_m＝（－40.00×10³－4.00×10³）J＝－44.00×10³J

Δ_rA_m和Δ_rG_m也可以由最大功求得

Δ_rA_m＝W_R＝＋W_R′

而由Δ_rU_m＝Q_R＋W_R＝Q_R＋W_R′＋与Δ_rU_m＝Q_p＋可得

W_R′＝Q_p－Q_R

所以

Δ_rA_m＝+Q_p－Q_R

   ＝（－2.48×10³－40.00×10³－4.00×10³）J

   ＝－46.48×10³J

Δ_rG_m＝W_R′＝－44.00×10³J

四、ΔG与温度的关系

在研究化学反应问题时，常需由某一反应温度（T₁）下的ΔG（T₁）求得另一反应温度（T₂）下的ΔG（T₂），二者之间的关系讨论如下。

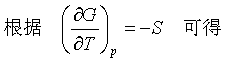
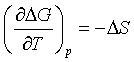
在温度T时，有

ΔG＝ΔH－TΔS   或    －ΔS＝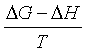

代入上式，得

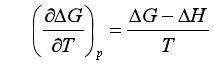 （54）

此式左边表示一个等温等压化学反应的ΔG在保持压力不变时对温度的变化率。将式（54）两边同除以T，并整理后可得

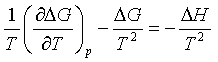
上式左方是压力不变时，（ΔG/T）对T的偏微商，即

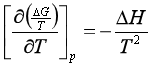（55）

对上式作不定积分，得

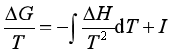（56）

式中I是积分常数。

若对式（55）进行定积分，则有

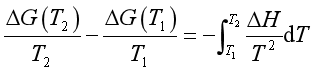(57)

以上三式称为吉布斯—亥姆霍兹（Gibbs-Helmholtz）方程式。若已知ΔH及某温度(T₁)下的ΔG(T₁)，便可应用本方程的积分形式(56)或(57)求得另一温度(T₂)下的ΔG(T₂)。

根据式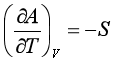，同样可以证明

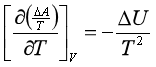（58）

该式也称为吉布斯——亥姆霍兹方程式。等式左方是体积不变时，（ΔA/T）对T的偏微商。与式(2.57)类似的推导,可由系统T₁温度下的ΔA(T₁)计算另一温度T₂下的ΔA(T₂)。

例11 氨的合成

N₂(g)+H₂(g)=NH₃(g)

已知当各种气体的温度为298.2K和分压均为时，

=-46.19kJ·mol^-1， =-16.63kJ•mol^-1。求1000K时的

解：因与温度有关，故应先求得对T的函数表达式，查表得各物质的C_p,m，可得：

△_rC_p=(-25.46+18.33×10^-3T/K-2.05×10⁵T^-2K²) JK^-1mol^-1

所以=∫△_rC_pdT+△H₀（△H₀为积分常数）
      =△H₀- (25.46T/K+×18.33×10^-3T²/K²-2.05×10⁵T^-1K) Jmol^-1

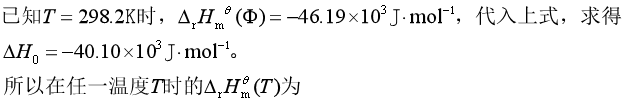
将代入吉布斯—亥姆霍兹方程式的不定积分式（2.56），得
           

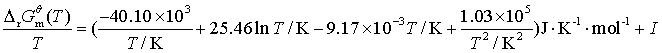
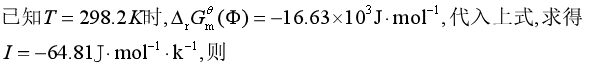
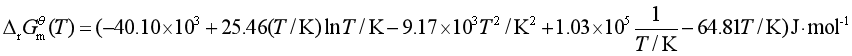
计算结果说明，在所给定的条件下，298.2K时合成氨的反应是自发的，有可能实现。但在1000K时，反应不能自动进行。

五、ΔG与压力的关系

一个等温等压下的化学变化或相变化，在保持温度不变的前提下，其ΔG将随压力的改变而改变。

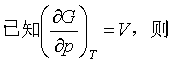
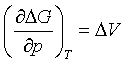
作定积分，得  

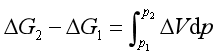
ΔG₁和ΔG₂分别是系统在同一温度，在两个不同压力下按等温等压进行时吉布斯自由能的变化。

例12  298K和下，相变

C（石墨）→C（金刚石）

＝2862J·mol^-1。已知石墨与金刚石的密度分别为2260 kg·m^-3和3515kg·m^-3。问需加压力至多大才能使变化成为自发？

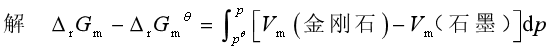
若密度与压力无关，则Vm可视为常量，便有

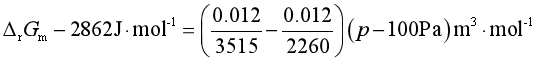
要使该相变化在等温等压下成为自发，则必须Δ_rG_m<0，即

2862 J·mol^-1-1.896×10^-6（p-100Pa）m³＜0

解得     p＞1.51×106Pa

压力必须大于1.51×106Pa才有可能使变化在298.2K，即室温时成为自发变化。