本章通过卡诺定理引入了熵的概念及克劳修不等式，定义了亥姆霍兹自由能和吉布斯自由能两个辅助热力学函数，导出了封闭系统中热力学基本公式，对应系数关系式和麦克斯韦关系式以及克拉贝龙方程等一系列重要的热力学公式，简要介绍了熵的统计意义和热力学第三定律。通过本章内容的学习，可以了解各种变化过程中、、等热力学函数改变值的计算，以及如何运用它们判别自发变化的方向，学会运用热力学基本原理演绎平衡系统性质的方法，为学习多组分系统和相平衡系统等后续内容奠定基础。

一、基本内容

（一）热力学第二定律的经典表述

开尔文说法：“不可能从单一热源取出热使之完全变为功，而不引起其他变化。”此表述也可说成：“第二类永动机不可能造成。”

克劳修斯说法：“不可能把热从低温物体传到高温物体，而不引起其他变化。”

（二）卡诺定理

工作在两个给定的热源之间的任何热机，其热机效率不可能超过卡诺热机的效率。设从高温热源吸热，对外做功为，向低温热源放热，则

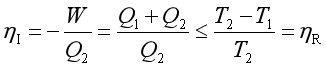
由此式可以得到

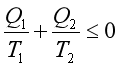
“=”表示可逆，“<”表示不可逆。即在指定的低温热源和高温热源之间，一切可逆循环的热温商之和等于零，一切不可逆循环的热温商之和小于零。

（三）熵的概念及其统计意义

熵变是可逆过程中的热温商之和

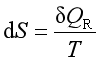或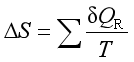

熵具有统计意义，它是系统微观状态数（或混乱度）的量度，这一关系可由玻耳兹曼公式给出

式中为玻耳兹曼常量，。

（四）克劳修斯不等式

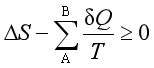或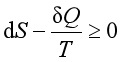

上式称为克劳修斯不等式，并作为热力学第二定律的数学表达式。将此式应用于绝热系统（或隔离系统）时得到

或

此式称为熵增加原理。

（五）熵变的计算

根据熵变的定义，不论实际过程可逆与否，封闭系统的熵变都可用下式计算

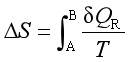
对于一些常见过程，计算熵变的公式有

1．简单状态变化：组成不变的封闭系统，在无相变化、化学变化（只是，，变化）的情况下，熵变为

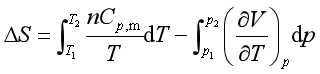
或                     

 

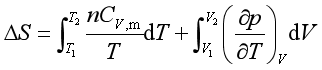
对理想气体，代入状态方程式，积分可得

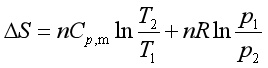
或                     

   

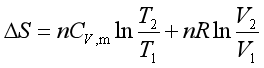
2．理想气体混合：在等温等压条件下，理想气体A和理想气体B混合过程的熵变为

3．相变化：相变过程分为可逆相变和不可逆相变两类。可逆相变的熵变为

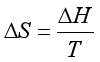
对于不可逆相变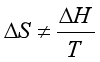，，需根据始终状态设计成可逆过程后再计算。

4．化学变化：对于化学反应的熵变计算有以下几种：

（1）设计成可逆电池反应，得。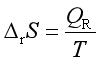

（2）已知某一温度（T₁）下的，求另一温度（T₂）下的。

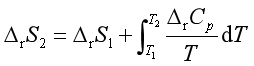
（3）利用物质的标准摩尔熵求算标准摩尔反应熵变

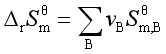      （产物为正，反应物为负）

（六）亥姆霍兹自由能A和吉布斯自由能G

    

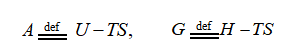
和均是系统的容量性质，具有能量的量纲。

（七）变化的方向和平衡条件

1．熵判据                   

2．亥姆霍兹自由能判据     

3．吉布斯自由能判据       

“<”表示变化自发，“=”表示达平衡。

（八）热力学函数间的关系式

1．热力学基本公式

四个热力学基本公式适用于组成不变的，不做非体积功的封闭系统。

2．对应系数关系式

        
              

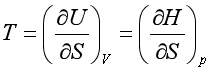
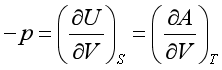
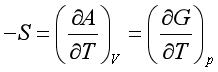
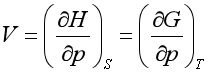
3．麦克斯韦关系式

        
        

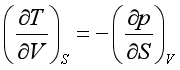
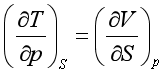
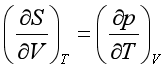
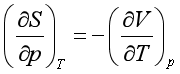
（九）和的计算

这里只涉及等温过程中和的计算。

1．简单状态变化

只要知道了和的关系或物态方程，即可求出和。

2．相变过程

相变一般是在等温等压下进行的，对可逆相变，；对不可逆相变，设计可逆过程来计算。其中所设计的可逆过程中，包含着可逆相变和简单状态变化的步骤。

3．化学反应

等温下的化学反应

利用化学反应等温式和标准摩尔生成吉布斯自由能计算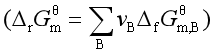将在“第五章化学平衡”中介绍。

（十）与温度和压力的关系

随温度变化的关系式为

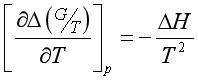
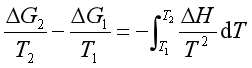
此式称为吉布斯-亥姆霍兹公式。

随压力变化的关系为

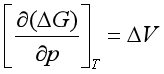
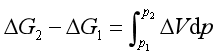
（十一）热力学第三定律

修正的普朗克说法：纯物质完美晶体在热力学温度零度时，熵（量热熵）为零。即

根据热力学第三定律，求得纯物质B在某一状态的熵称为该物质B在该状态的规定熵。在标准状态下温度时的规定熵，称为物质B在时的标准熵。

二、重点与难点

（一）自发变化

1．自发变化的共同特征

自发变化是指能够自动发生的变化，即不需要环境对系统做功就能发生的变化。而自发变化的逆向变化称为非自发变化，它必须依靠环境对系统做功才能进行。

自发变化的共同特征：（1）具有一定的方向和限度；（2）具有对环境做功的能力。

系统在进行自发变化时将失去一些做功能力，进行过程中可以做功，也可以不做功。而非自发变化进行时必须由其他自发变化提供功，同时获得一定的做功能力。

2．变化的方向性与过程的可逆性

在指定的始态A和终态B之间，判别A→B为自发变化，还是B→A为自发变化，这就是所谓的变化的方向性，也是热力学第二定律所要解决的核心问题。

系统经过某一过程，由始态A变到终态B之后，若能使系统和环境都完全复原，则此过程称之为可逆过程。反之为不可逆过程，这便是过程的可逆性问题。

变化是否自发取决于系统的始、终两态，而过程的可逆与否取决于对过程的具体安排，两者之间并无必然的联系。不论是自发变化或非自发变化，都可以可逆进行或不可逆进行。

（二）熵

1．熵的概念和克劳修斯不等式

在对卡诺热机效率的讨论证明中引出了热力学第二定律，通过对卡诺定理的引伸发现了热力学熵函数。熵变的定义用下式表示

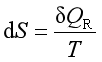   或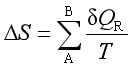   

熵是系统的容量性质，单位是。应用熵的定义将卡诺定理推广到任意不可逆循环过程，可以导出克劳修斯不等式

注意：克劳修斯不等式是用来判断过程的可逆性，在环境不对系统做功的条件下，可以用来判断变化的方向。

将克劳修斯不等式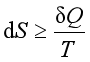应用于绝热系统（或隔离系统），得到，“=”表示可逆，“>”表示不可逆。注意：利用判断过程的可逆性只限于绝热系统（或隔离系统），而在隔离系统中可以用判断变化的方向，即表示自发，表示平衡。

2．熵的统计意义

从微观角度看，熵是系统微观状态数的量度，微观状态数越大，熵越大；反之则熵越小。联系熵与微观状态数的关系式称为玻耳兹曼关系式

此式是联系宏观与微观的桥梁。利用此式可以对一些物质的熵值大小作定性的比较。

（1）同一种物质的气、液、固三态比较，。

（2）分子越大，结构越复杂，熵越大。分子数增加的反应，熵增大；反之，分子数减少的反应，熵减小。

（3）对同一种物质的同一聚集状态而言，温度高者熵大。对一定量的气体而言，低压时熵大。

3．熵变的计算

熵变的计算是本章的难点之一，对简单过程的熵变计算，请参照前面“一、基本内容”中的熵变计算。对一些较复杂的过程，往往是由一些简单过程通过某种方式组合而成，这里仅介绍计算熵变的大体思路以供参考。

（1）根据所给条件，确定系统的始态和终态。

（2）在指定的始终态之间设计一可逆过程，求此可逆过程的热温商之和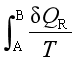，过程设计往往需要一定的技巧。

（3）对于有些不可逆过程，可利用熵是状态函数这一特点，从可逆过程计算的结果中直接给出。例如，理想气体在温度T时由体积等温可逆膨胀至，则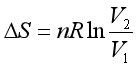。若理想气体从相同的始态经自由膨胀至相同的终态，则熵变相同。

（三）亥姆霍兹自由能A和吉布斯自由能G

1．A和G的物理意义

A和G都是系统的状态函数，是系统的容量性质，具有能量的量纲，但不是能量。尽管是在等温条件下导出的，但不是说只有在等温条件下才有，只要有状态变化，就有，只不过此时的不等于可逆过程中的功。

同样对G应按来理解其物理意义，在等温等压可逆过程中，系统吉布斯自由能的变化等于系统所做的非体积功，即；在等温等压不可逆过程中，系统自由能的变化小于系统所做的非体积功，即。

2．和的计算

参见“一、基本内容”中的和的计算，对于简单状态变化、相变化和化学变化要用不同的计算公式。实际上，只要是等温变化，都可以利用、来计算，只是计算过程略复杂而已，需分别计算和。

对于变温过程，通常利用吉布斯—亥姆霍兹公式计算。

3．变化方向性的和判据

以判据为例

（1）若，则，即对于的变化，不论以何种方式（可逆和不可逆）进行时，都必须消耗环境的非体积功（数值上至少等于）才能进行。故的变化为非自发变化。

（2）若，则，即对于的变化不仅不需要环境做功，而且系统还具有对环境做功的能力（最大值为）。故的变化为自发变化。

同理可以说明的变化为自发变化，的变化为非自发变化。综上所述，变化方向性的和判据分别为

           

（四）热力学证明题

1．数学准备

解答热力学证明题常用的数学公式有以下几个：

（1）循环关系式

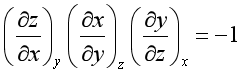
（2）倒易关系式

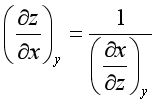
（3）求导次序无关定理

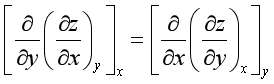
（4）链关系         

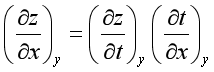
2．偏微商的处理方法

热力学证明题中常涉及到一些热力学函数的偏微商，通常先利用数学公式处理，再利用热力学关系进行变量替换。如果以、代表、、、；代表、、、，则对以下三种类型的偏微商处理方法是：

（1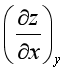）型。通常由热力学基本方程出发，在下角标量规定的条件下，以微分相除法处理。例如，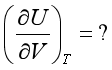

由，得

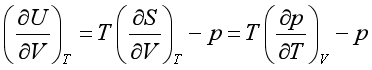
（2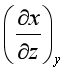）型。先利用倒易关系或链关系，再利用热力学关系式。例如，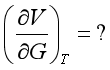

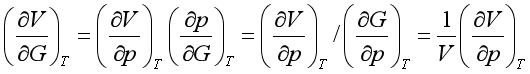
（3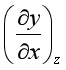）型。先利用循环关系，再利用热力学关系式。例如，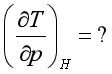

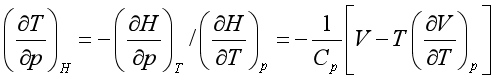
含熵的偏微商也可以利用可测量的物理量、、、、等表示。例如

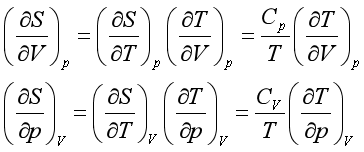
对于其他含熵的偏微商，如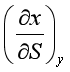和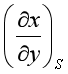，也可利用链关系或循环关系进行处理。