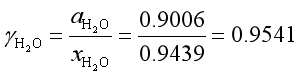第三章 多组分系统热力学
 知识点八:实际液态混合物和实际溶液
知识点八:实际液态混合物和实际溶液
一、实际液态混合物对理想液态混合物的偏差
对于理想液态混合物,由于溶剂和溶质都遵守拉乌尔定律,因此其饱和蒸气压与组成之间是线性关系。此时,形成溶液时![]() 。对于理想稀溶液,溶剂服从拉乌尔定律,溶质服从亨利定律,故蒸气压与组成的关系,在“稀溶液”浓度范围里,也是线性关系。这两种理想情况毕竟是少数,对大部分情况下,形成液相系统时,分子间作用力与纯态时不同,因而
。对于理想稀溶液,溶剂服从拉乌尔定律,溶质服从亨利定律,故蒸气压与组成的关系,在“稀溶液”浓度范围里,也是线性关系。这两种理想情况毕竟是少数,对大部分情况下,形成液相系统时,分子间作用力与纯态时不同,因而![]() 。
。
实际液态混合物对理想系统的偏差,在二元系统中可用图形表示,如果A,B两组分形成液态混合物,分子间的作用力![]() ,存在如下一些情况
,存在如下一些情况![]() ,
,![]() ,这时
,这时![]() ,
,![]() ,所以
,所以![]() ,
,![]() 与
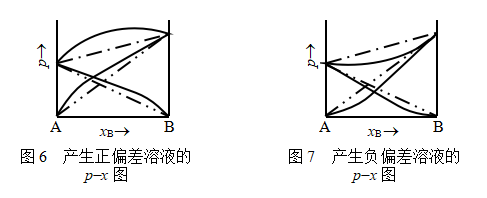
与![]() 也不可能是线性关系,如图6所示。这种情况称作对拉乌尔定律产生了“正偏差”,形成这类液态混合物时,总伴随着吸热和体积增加。
也不可能是线性关系,如图6所示。这种情况称作对拉乌尔定律产生了“正偏差”,形成这类液态混合物时,总伴随着吸热和体积增加。
如果A和B形成液态混合物时,组分发生解离或原缔合分子变为单分子,也会发生上述情况。
若A,B形成液态混合物时,![]() ,
,![]() ,则
,则![]() ,
,![]() ,故
,故![]() ,这种情况称为对拉乌尔定律产生了负偏差,如图7所示。形成这类溶液时,总伴随着放热和体积缩小(即
,这种情况称为对拉乌尔定律产生了负偏差,如图7所示。形成这类溶液时,总伴随着放热和体积缩小(即![]() < 0,
< 0,![]() < 0)。若A,B形成液态混合物时,组分发生缔合,也会发生负偏差。
< 0)。若A,B形成液态混合物时,组分发生缔合,也会发生负偏差。
在绝大多数情况下,若一个组分对拉乌尔定律发生正偏差,另一个组分必然也对拉乌尔定律发生正偏差。若一个组分对拉乌尔定律发生负偏差,则另一个组分必对拉乌尔定律发生负偏差。但有一些实际系统并不遵循此规律,例如,C2H5OH-CHCl3系统,CHCl3在整个浓度范围内发生正偏差,而C2H5OH在x2<0.38时发生正偏差,在x2>0.38时发生负偏差,这可从键偶极及超额函数得到解释。
实际溶液的情况也各有不同,它既与溶剂、溶质的性质有关,也与温度、压力、溶液的浓度有关,如何用热力学方法来处理它是很复杂的。因为若把理想系统的公式直接用于实际溶液系统,则所得结果与实验结论相差甚大。而若对每一个实际溶液进行个别的,而非普遍性的讨论又太繁琐且无普遍意义。
二、活度、活度因子及实际液态混合物中组分的化学势
为了使实际系统的热力学关系简单化,与处理实际气体引进逸度相类似,对实际液态混合物中的各组分和实际溶液中的溶剂与溶质,路易斯提出了“活度”的概念,并应用于实际液态系统化学势的表达式,即对理想系统中组分的化学势表达式加以修正,用活度代替组分的组成或浓度,就可以准确地反映实际情况。
修正的实际液态系统化学势表达式必须满足两点:(1)物质化学势的表达式能保持理想系统组分化学势表达式的数学形式;(2)实际体系中组分化学势表达式在极限情况下“还原”成理想系统中组分化学势的表达式。
理想液态混合物中任一组分化学势的表达式为
为了借鉴上述形式,将实际液态混合物中任一组分B的化学势的表示为
![]() (55)
(55)
![]() 称为B组分的活度,是量纲一的量,并定义
称为B组分的活度,是量纲一的量,并定义
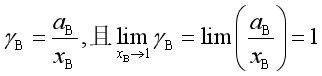 (56)
(56)
则
![]() (57)
(57)
![]() 称为活度因子,它也是量纲一的量。
称为活度因子,它也是量纲一的量。![]() 表示实际混合物中,B组分的摩尔分数与理想液态混合物的偏差。
表示实际混合物中,B组分的摩尔分数与理想液态混合物的偏差。
式(55)中的![]() 是
是![]() ,
,![]() ,即
,即![]() 的那个状态的化学势,该状态即是纯组分B在温度T,压力p时的化学势,是一个真实存在的状态。
的那个状态的化学势,该状态即是纯组分B在温度T,压力p时的化学势,是一个真实存在的状态。
在SI单位之中,引入了绝对活度![]() 的概念,定义绝对活度
的概念,定义绝对活度
![]() (58a)
(58a)
或
![]() (58b)
(58b)
绝对活度也是量纲一的量。
同样有纯物质B的绝对活度为
![]() (59a)
(59a)
或
![]() (59b)
(59b)
以及物质B的标准绝对活度
![]() (60a)
(60a)
或
液态混合物中任一组分B的标准绝对活度![]() 为相同温度及标准压力下,纯液体B的绝对活度,即
为相同温度及标准压力下,纯液体B的绝对活度,即![]() 。
。
将式(58b)和式(59b)代入实际液态混合物中任一组分的化学式表达式,即式(55)可得
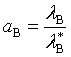 (61)
(61)
故组分B的活度![]() 又称为相对活度。
又称为相对活度。
定义了绝对活度之后,就可以用绝对活度定义活度、活度因子等物理量,所有有关化学势的表示式也都可以转换成绝对活度表示的关系式,这样处理可能会带来许多方便。但因传统习惯的原因,人们仍沿用相对活度的概念及与其相关的各种表达式。
三、实际稀溶液
若溶质是气体或固体,溶剂是液体;或溶剂、溶质都是液体,但彼此部分互溶。对于这种溶剂溶质要区分的系统,其理想化的情况就是理想稀溶液。理想稀溶液中溶剂化学势的表达式是(35),溶质化学势的表达式是(38)、(41)、(46)。故在实际溶液系统中,溶剂化学势的表达式按拉乌尔定律进行修正,溶质化学势的表达式按亨利定律进行修正。
按拉乌尔定律进行修正后,溶剂化学势应为
![]() (62)
(62)
或
![]() (63)
(63)
![]() 是溶剂A的活度因子,
是溶剂A的活度因子,![]() 是溶剂的活度,式(63)与(55)一致,故活度的定义与(56)一致。溶剂化学势的标准态是指定
是溶剂的活度,式(63)与(55)一致,故活度的定义与(56)一致。溶剂化学势的标准态是指定![]() 下液体纯溶剂,这是一个真实纯态。
下液体纯溶剂,这是一个真实纯态。
若溶质浓度用质量摩尔浓度m表示时,实际溶液中溶质的化学势应按式(42)进行修正,即为
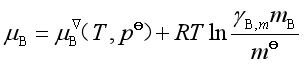
或
![]() (64)
(64)
式中
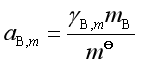 (65)
(65)
化学势的标准态是![]() ,且又服从亨利定律(
,且又服从亨利定律(![]() )的假想状态(参阅图3b),
)的假想状态(参阅图3b),![]() 就是标准态时溶质的化学势。
就是标准态时溶质的化学势。
这种情况时活度的定义为
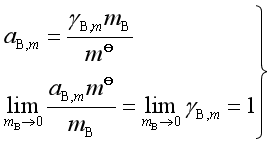 (66)
(66)
当溶质浓度用摩尔分数x表示时,溶质化学势的表达式按(41)进行修正
修正后
或
![]() (67)
(67)
其中
![]() (68)
(68)
![]() 是溶质浓度用摩尔分数表示时的活度,
是溶质浓度用摩尔分数表示时的活度,![]() 是相应的活度因子。
是相应的活度因子。
选取![]() ,此时
,此时![]() =1的状态作为溶质B的化学势的标准态。这个状态是指定
=1的状态作为溶质B的化学势的标准态。这个状态是指定![]() 和
和![]() 下的纯B(
下的纯B(![]() )且又服从亨利定律(
)且又服从亨利定律(![]() )的状态(参阅图3a)。这个假想状态的化学势是
)的状态(参阅图3a)。这个假想状态的化学势是![]()
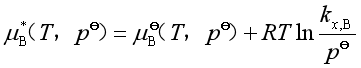
它与理想稀溶液中溶质在标准态时的化学势一致。
所以,当溶质浓度用摩尔分数x表示时,活度的定义是
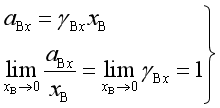 (69)
(69)
若溶质的浓度用物质的量浓度c表示,实际溶液中B组分的化学势应按式(43)进行修正,即
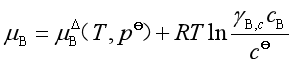
或
![]() (70)
(70)
式中
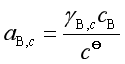 (71)
(71)
化学势的标准态是![]() 且又服从亨利定律的假想状态,(参阅图3c),
且又服从亨利定律的假想状态,(参阅图3c),![]() 是标准态时溶质的化学势。
是标准态时溶质的化学势。
活度的定义是
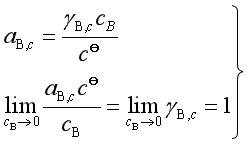 (72)
(72)
四、活度的测定
1.蒸气压法
对按拉乌尔定律修正的组分来说应有
![]() (73)
(73)
所以
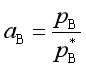 (74a)
(74a)
或
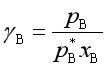 (74b)
(74b)
溶液中的溶质是对亨利定律进行修正的,若溶质浓度用质量摩尔浓度![]() 表示,则有
表示,则有
![]() (75)
(75)
则
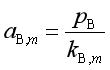 (76a)
(76a)
或
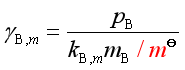 (76b)
(76b)
由以上各式可知,若测得某组分的蒸气压,又已知它们的饱和蒸气压或溶质的亨利系数,便可计算它们的活度或活度因子。若溶质的浓度用![]() 或
或![]() 表示,也可得类似式(76)的结果。
表示,也可得类似式(76)的结果。
例10 298K时,纯水的饱和蒸气压是3.167kPa,水溶液中水蒸气的平衡分压是2.733kPa,若选298K下纯水的真实状态作标准态,求溶液中水的活度。若选298K下与0.133kPa水蒸气达平衡时的假想纯水作标准态,求溶液中水的活度。
解 第一种情况下
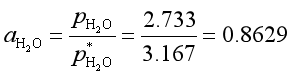
第二种情况下
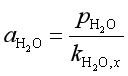
在假想纯态时 ![]()
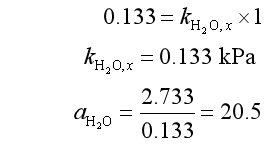
可见,活度![]() 是相对活度,其数值与所取标准态有关。
是相对活度,其数值与所取标准态有关。
2. 凝固点下降法测溶剂活度
在讨论稀溶液凝固点降低时曾得
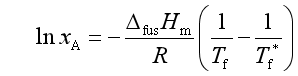
对实际溶液中的溶剂组分,用活度代替浓度,可得到
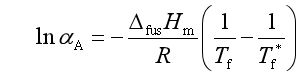 (77)
(77)
若测得实际溶液的凝固点,可求得溶剂的活度。
例11 262.5K时,饱和KCl溶液(1000g水中含KCl为3.30mol)与纯水共存,已知水的凝固焓为-5.858kJ·mol-1,若以纯水为标准态,计算饱和溶液中水的活度及活度因子。
解 由凝固点下降公式
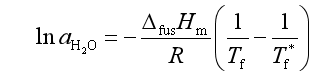
代入 ![]()
可得![]()
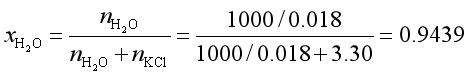
所以