一、基本内容
本章是热力学基本原理在化学反应中的具体应用,包括三个方面的内容:
(1)用热力学方法讨论一定条件下化学反应进行的方向和限度。
(2)用热力学方法确定化学反应达到平衡时系统的组成,即用热力学和热化学数据来计算反应系统的平衡常数。
(3)根据热力学原理推导出反应的等温方程和等压方程,从而定量地解决一定条件下反应系统平衡移动的规律,以便更好地指导生产。
(一)反应进行方向的判据
在封闭系统中有一反应
若在等温等压条件下,反应发生了反应进度为d![]() 的变化,系统内吉布斯自由能的变化应为
的变化,系统内吉布斯自由能的变化应为
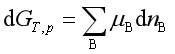
因为 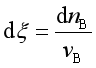 ,所以
,所以 ![]() 。
。
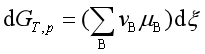 或
或 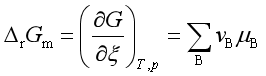
![]() 表示在等温等压下,在无限大量系统中(
表示在等温等压下,在无限大量系统中(![]() 不随
不随![]() 而变),反应按计量方程进行一个单位反应进度时系统吉布斯自由能的改变,称为摩尔反应吉布斯自由能,其单位是J·mol-1。
而变),反应按计量方程进行一个单位反应进度时系统吉布斯自由能的改变,称为摩尔反应吉布斯自由能,其单位是J·mol-1。
若![]()
![]() 0,即
0,即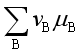
![]() 0,表示反应在指定的温度
0,表示反应在指定的温度![]() 、压力
、压力![]() 及反应进度
及反应进度![]() 时反应能自发地自左向右进行。
时反应能自发地自左向右进行。
若![]()
![]() 0,即
0,即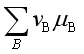
![]() 0,表示反应在指定的温度
0,表示反应在指定的温度![]() 、压力
、压力![]() 及反应进度
及反应进度![]() 时反应自发地自右向左进行。
时反应自发地自右向左进行。
若![]() =0,即
=0,即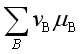 = 0,表示反应在指定的温度
= 0,表示反应在指定的温度![]() 、压力
、压力![]() 及反应进度
及反应进度![]() 时,反应达到平衡。
时,反应达到平衡。
所以反应进行方向的判据是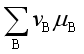 值,但由于其计算不方便,故导出反应的等温方程。
值,但由于其计算不方便,故导出反应的等温方程。
(二)化学反应的等温方程
依据任何系统的化学势的表达式可以写为![]() 及平衡条件
及平衡条件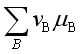 = 0,可推出等温方程
= 0,可推出等温方程
式中![]() 为标准平衡常数,Qa称为活度商,它是指定
为标准平衡常数,Qa称为活度商,它是指定![]() 时系统各组分活度幂次方之积。
时系统各组分活度幂次方之积。
若![]() >
>![]() , 则
, 则![]() <0,反应自发自左向右进行;
<0,反应自发自左向右进行;
若![]() <
<![]() , 则
, 则![]() >0,反应自发逆向进行;
>0,反应自发逆向进行;
若![]() =
=![]() , 则
, 则![]() =0,反应达到平衡。
=0,反应达到平衡。
反应的等温方程表示等温、等压条件下,在无限大量系统中进行一个单位反应时系统吉布斯自由能的改变。在有限量系统中,它只能作为反应进行到某个![]() 时,反应继续进行方向的判据。
时,反应继续进行方向的判据。
(三)标准平衡常数与经验平衡常数
因 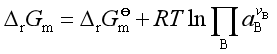 ,达平衡时
,达平衡时 ![]() , 所以
, 所以
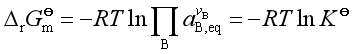 ,
, ![]() 称为标准平衡常数。不同的系统标准平衡常数的表示有所不同。
称为标准平衡常数。不同的系统标准平衡常数的表示有所不同。
1. 理想气体反应系统
对于理想气体反应
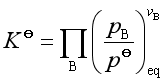
除了标准平衡常数外,理想气体反应还有经验平衡常数Kp, Kc, Kx ,它们分别是
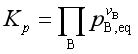 ;
;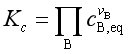 ;
;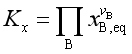
它们之间的关系是
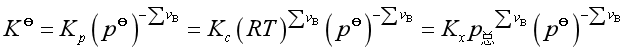
当![]() 时,标准平衡常数与各经验平衡常数的量值相等,但
时,标准平衡常数与各经验平衡常数的量值相等,但![]() 与Kx是量纲一的量,Kp、 Kc的单位分别为
与Kx是量纲一的量,Kp、 Kc的单位分别为![]() 和
和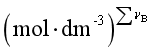 ;
;![]() 、Kp、Kc都仅与温度有关,只有Kx与温度和总压有关。
、Kp、Kc都仅与温度有关,只有Kx与温度和总压有关。
2. 实际气体反应系统
标准平衡常数 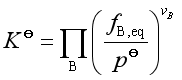
经验平衡常数 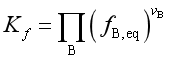
![]() 称为逸度。
称为逸度。![]() 只是温度的函数,与压力无关。而
只是温度的函数,与压力无关。而![]() 不仅与温度有关,还与压力有关。
不仅与温度有关,还与压力有关。
3. 液态混合物的反应系统
若系统可看成是理想液态混合物,则
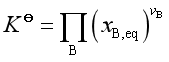
其经验平衡常数是Kx,量值与![]() 相等。
相等。
若系统是非理想的,标准平衡常数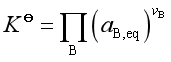 。其经验平衡常数为
。其经验平衡常数为![]() 。
。![]() 与
与![]() 在量值上相等,但
在量值上相等,但![]() 只是温度的函数,而
只是温度的函数,而![]() 与温度,压力有关,但压力对其影响不大。
与温度,压力有关,但压力对其影响不大。
4. 稀溶液的系统
若参与反应的物质溶于同一溶剂中,并与溶剂构成理想稀溶液,其标准平衡常数
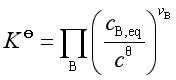
经验平衡常数是![]() ,
,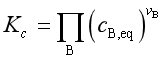 。
。
若系统是非理想的稀溶液,其标准平衡常数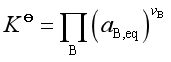
该系统的![]() 常称为“杂”平衡常数,因为参与反应的各物质的标准态并非一致。
常称为“杂”平衡常数,因为参与反应的各物质的标准态并非一致。
5. 复相反应系统
若参与复相反应的各凝聚物之间不组成溶液或熔体,气体可当作理想气体,则其标准平衡常数
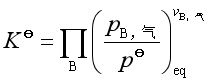
式中![]() 是指参与复相反应的气体物质的分压,可见在标准平衡常数的表达式中不出现凝聚物的浓度。其经验平衡常数是
是指参与复相反应的气体物质的分压,可见在标准平衡常数的表达式中不出现凝聚物的浓度。其经验平衡常数是![]() ,
,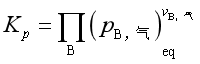 。
。
若参与复相反应的各凝聚物之间形成溶液或熔体,气体可当作理想气体,如反应
则其标准平衡常数为,
则 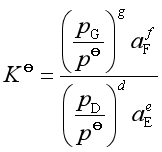
显然,这里的![]() 也是“杂”平衡常数。
也是“杂”平衡常数。
(四)反应的标准摩尔吉布斯自由能![]()
等温等压下,在无限大量系统中参与反应的各物处于各自的标准态时,单位反应的吉布斯自由能变化叫作反应的标准摩尔吉布斯自由能变化,简称标准摩尔吉布斯自由能,记作![]() ,单位是
,单位是![]() 。
。
该式说明通过热力学数据得到![]() ,便可计算得到
,便可计算得到![]() ,比用实验测定平衡时各物质的浓度去计算平衡常数方便得多。
,比用实验测定平衡时各物质的浓度去计算平衡常数方便得多。
要注意上式在数学上是严格相等的,但所表示的状态是不完全一致的,左边表示反应的各物质处于各自的标准态,而右边![]() 表示反应达平衡时各物的活度(或分压)积,标准态不一定是平衡态,故两者不能混为一谈。
表示反应达平衡时各物的活度(或分压)积,标准态不一定是平衡态,故两者不能混为一谈。![]() 不能用作反应趋势的判据,但
不能用作反应趋势的判据,但![]() 的值可用于反应限度的依据。
的值可用于反应限度的依据。
(五)化合物的标准生成自由能
定义:一定温度下,由稳定单质生成![]() 的物质B的标准摩尔吉布斯自由能变化,称为物质B的标准摩尔生成吉布斯自由能,记作
的物质B的标准摩尔吉布斯自由能变化,称为物质B的标准摩尔生成吉布斯自由能,记作![]() ,单位是
,单位是![]() 。
。
任一反应的![]() 可通过
可通过![]() 求得
求得
(六)温度对化学平衡的影响
温度对化学平衡的影响是因为温度影响了平衡常数的大小,从而改变了平衡组成。
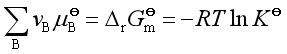
因为![]() 与温度有关,故
与温度有关,故![]() 与温度有关,定量关系由范托夫等压式表示
与温度有关,定量关系由范托夫等压式表示
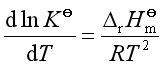
式中:![]() 是反应的标准摩尔焓变,它可由参与反应的标准摩尔生成焓计算得到。
是反应的标准摩尔焓变,它可由参与反应的标准摩尔生成焓计算得到。
对于等温等压下的吸热反应,![]() >0,故
>0,故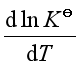 >0,随温度升高,平衡右移,有利于反应正向进行。
>0,随温度升高,平衡右移,有利于反应正向进行。
对于等温等压下的放热反应,![]() <0,则
<0,则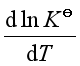 <0,随温度升高,平衡左移,不利于反应正向进行。
<0,随温度升高,平衡左移,不利于反应正向进行。
(七)压力对平衡的影响
压力对理想气体反应的平衡常数![]() 有影响,所以影响平衡组成,使平衡移动。
有影响,所以影响平衡组成,使平衡移动。
对于理想气体反应系统
因 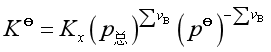
经数学处理,可得 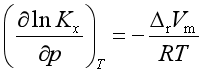
![]() 是单位反应中产物的体积与反应物体积之差,故若反应
是单位反应中产物的体积与反应物体积之差,故若反应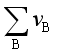 >0,则
>0,则![]() >0,即随压力的升高Kx减少,平衡逆向移动;若反应
>0,即随压力的升高Kx减少,平衡逆向移动;若反应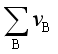 <0,
<0,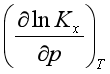 >0,即随压力的升高Kx增大,平衡正向移动。总的说来,压力升高有利于分子数减少的反应。
>0,即随压力的升高Kx增大,平衡正向移动。总的说来,压力升高有利于分子数减少的反应。
由于凝聚相反应在反应前后体积改变不大,故压力对凝聚相反应影响不大,除非压力很大。
(八)溶液反应的标准摩尔反应吉布斯自由能![]()
溶液反应的标准摩尔吉布斯自由能变化不能由化合物的标准摩尔生成吉布斯自由能直接计算得到,因为标准摩尔生成吉布斯自由能是每个化合物在纯态时的![]() ,而对于溶液反应的各种物质显然是不合适的。
,而对于溶液反应的各种物质显然是不合适的。
设有溶液反应
若溶液中各物质的浓度用物质的量浓度表示,则反应的标准摩尔吉布斯自由能变化为
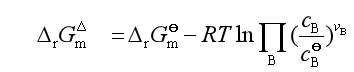
式中: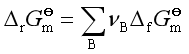 ,它可直接查各化合物的
,它可直接查各化合物的![]() 值计算得到;
值计算得到;![]() 是各物质的饱和溶解度。
是各物质的饱和溶解度。
(九)同时平衡
同一化学反应系统里若有若干个独立反应同时进行,彼此有一种或一种以上相同的反应物或产物,当反应系统达到平衡时,就叫作同时平衡。
反应自发进行的判据是![]() ,A是反应的亲和势。若反应系统有两个独立反应达到同时平衡,即有两个反应,若
,A是反应的亲和势。若反应系统有两个独立反应达到同时平衡,即有两个反应,若

故同时平衡的条件是每个反应的亲和势均为0。
当系统达到同时平衡时,每一种相同的反应物或产物的浓度(或分压)在各个反应中均为同一数值,这是计算原则。
二、重点与难点
1. 化学反应的等温方程是判断在定温、定压及已指定反应进度时反应进行方向和限度的判据,因此必须牢牢掌握。应该熟悉不同反应系统中等温方程的表达式,以方便使用。
用等温方程式来计算单位反应的吉布斯自由能变化只能应用于无限大量的反应系统。在有限量系统中,等温方程只能用作判据。
2. 掌握各个反应系统标准平衡常数的表达式是本章的基础,熟悉![]() 与经验平衡常数间的换算,熟练掌握平衡常数的计算方法。
与经验平衡常数间的换算,熟练掌握平衡常数的计算方法。
3. 掌握温度对平衡常数的影响并能熟练的应用范荷夫等压方程式的定积分形式、不定积分形式进行不同温度下平衡常数的计算。
4. 压力及惰性气体对气相反应的影响可通过它们改变气相反应的平衡组成表现出来,应熟练掌握计算方法。
5. 同时平衡的计算是本章的难点,故应掌握其计算原则及方法。
6. 溶液(或熔体)反应中的![]() 的计算是本章的难点,由此而得的是“杂”平衡常数,在计算中常涉及活度问题。
的计算是本章的难点,由此而得的是“杂”平衡常数,在计算中常涉及活度问题。

