第七章 电解质溶液
知识点四:电解质溶液的平衡性质
一、电解质溶液中的离子平均活度和平均活度因子、离子强度
由于电解质在溶液中解离，产生阳离子和阴离子，这些离子之间存在着静电引力或斥力，所以电解质溶液对于理想溶液必然会产生不同程度的偏差，并且这种偏差比非电解质溶液对理想溶液的偏差要复杂一些。不过，在热力学的计算中，我们仍然用活度来衡量这种偏差。
对于任一电解质
来说，若它在溶液中按下式解离：
达解离平衡时，电解质
的化学势mB为阴、阳离子的化学势的代数和：
(27)
按活度的定义
，可得整体电解质的化学势及阳离子、阴离子的化学势分别为：
(28a)
(28b)
(28c)
式中aB、a+、a－分别为电解质、阳离子、阴离子的活度；
、
、
分别为相应的标准化学势。将式(28b)和(28c)式代入式(27)后整理得
(29)
上式与式(28a) 比较可见
(30)
(31)
式(31)就是电解质溶液中电解质的活度与阴、阳离子的活度间的关系。
但是，由于溶液总是电中性的，我们不可能制得只有阳离子或只有阴离子单独存在的溶液，因此单独离子的活度是无法直接由实验测得的。实验中能直接测量的是离子的平均活度，因此，我们定义电解质
的溶液中离子的平均活度
与阴、阳离子的活度间的关系为
(32)
其中，
。
于是得
(33)
(34)
而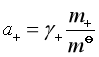 
，
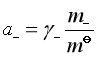
故 
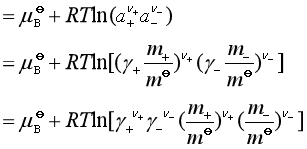
为了简化起见，我们再定义电解质溶液中离子的平均质量摩尔浓度
和平均活度因子
：
(35)
(36)
这样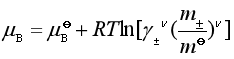 
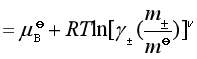
显然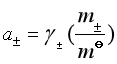 
(37)
这就保持了电解质溶液中离子的平均活度
与平均活度因子
间的简明关系，同时也说明了电解质必须使用平均活度因子
的原由。
若电解质
为强电解质，由于在溶液中它完全解离，溶液中不存在
这样的物种，而只存在着
和
。若该电解质的质量摩尔浓度为m，则溶液中离子的质量摩尔浓度为
，
，因此，该电解质的活度为
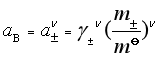
而 
所以强电解质(
)溶液在质量摩尔浓度为m时的活度为：
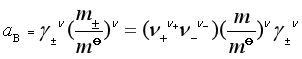(38)
若电解质
为弱电解质，并已知它在溶液中的解离度a，则该溶液中存在着确定量的物种
和确定量的阴、阳离子，因此，电解质
的活度aB是指物种
的活度，但
的离子活度因子仍指的是离子的平均活度因子
。
的值可用实验测定，表5列出了298.15K时水溶液中一些强电解质的离子平均活度因子的测定值，可应用此表计算电解质的离子平均活度。
表5 298.15K时水溶液中一些强电解质的离子平均活度因子
电解质 |
m/(mol |
||||||||
0.001 |
0.005 |
0.01 |
0.05 |
0.10 |
0.50 |
1.0 |
2.0 |
4.0 |
|
HCl |
0.965 |
0.928 |
0.904 |
0.830 |
0.796 |
0.757 |
0.809 |
1.009 |
1.762 |
HNO3 |
0.965 |
0.927 |
0.902 |
0.823 |
0.785 |
0.715 |
0.720 |
0.783 |
0.982 |
NaOH |
|
|
0.899 |
0.818 |
0.766 |
0.693 |
0.679 |
0.700 |
0.890 |
NaCl |
0.966 |
0.929 |
0.904 |
0.823 |
0.778 |
0.682 |
0.658 |
0.671 |
0.783 |
KCl |
0.965 |
0.927 |
0.901 |
0.815 |
0.769 |
0.650 |
0.605 |
0.575 |
0.582 |
H2SO4 |
0.830 |
0.639 |
0.544 |
0.340 |
0.265 |
0.154 |
0.130 |
0.124 |
0.171 |
K2SO4 |
0.89 |
0.78 |
0.71 |
0.52 |
0.43 |
0.26 |
0.21 |
|
|
CaCl2 |
0.887 |
0.783 |
0.724 |
0.574 |
0.518 |
0.448 |
0.500 |
0.792 |
2.934 |
CdCl2 |
0.819 |
0.623 |
0.524 |
0.304 |
0.228 |
0.100 |
0.066 |
0.044 |
|
BaCl2 |
0.88 |
0.77 |
0.72 |
0.56 |
0.49 |
0.39 |
0.39 |
|
|
CuSO4 |
0.74 |
0.53 |
0.41 |
0.21 |
0.16 |
0.068 |
0.047 |
|
|
ZnSO4 |
0.734 |
0.477 |
0.387 |
0.202 |
0.148 |
0.063 |
0.043 |
0.035 |
|
LaCl3 |
0.790 |
0.636 |
0.560 |
0.388 |
0.383 |
0.328 |
0.424 |
|
|
) 从表5所列数据可知：
(1)电解质的离子平均活度因子
与水溶液的浓度有关。在稀溶液范围内，
随浓度降低而增加，无限稀释时达极限值1；而在一般情况下
总是小于1，但当浓度增加到一定程度时，
值可能随浓度的增加而变大，甚至大于1。这是由于离子的水化作用，使较浓溶液中的许多水分子被束缚在离子周围的水化层内，不能自由移动，这相当于使溶剂量相对减少而造成的。
(2)在稀溶液范围内，对相同价型的电解质而言，浓度相同时，其
的值近乎相等；而不同价型的电解质，虽然浓度相等，但其
并不相同，高价型电解质的
较小。
1921年路易斯提出了离子强度的概念，并根据实验结果总结出了电解质溶液的离子平均活度因子
与溶液的离子强度I间的经验关系为
(39)
在给定温度和溶剂时，A´为常数。这个经验关系式只适用于I< 0.01mol
的电解质溶液。
离子强度I的定义如下：
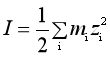(40)
式中，i为溶液中的任一离子，mi为i离子的质量摩尔浓度，zi为i离子的电荷数。因此离子强度I是一个量纲与质量摩尔浓度m相同的物理量，其大小反映了电解质溶液中离子间静电作用的强弱，是电解质溶液的性质偏离理想溶液性质的主要原因所在。离子强度的概念最初是从实验数据得到的一些感性认识中提出来的，后来，德拜－休克尔在理论推导中很自然地出现了与I有关的一项，并在理论上得到了类似于(39)式的计算公式，即德拜－休克尔极限公式。
二、强电解质溶液的离子互吸理论和德拜－休克尔极限公式
1923年，德拜和休克尔提出了能解释强电解质溶液性质的离子互吸理论，也称为非缔合式电解质理论。该理论认为，强电解质在溶液中是完全解离的，强电解质溶液与理想溶液的偏差，主要是由溶液中阴、阳离子之间的静电作用所引起的。
德拜－休克尔根据离子间静电作用与离子热运动的关系，提出了离子氛的概念。
强电解质溶液中阴、阳离子共存，整个溶液呈电中性。依据库仑定律，同性离子相互排斥，异性离子相互吸引，因此，整个溶液中的离子在静电力的作用下趋于规则地分布。但是，离子在溶液中的热运动则力图使它们随机地分布在溶液中。由于热运动不足以与相对强大的静电力相抗衡，所以在溶液中离子虽然不能完全有规则地分布，但从统计的角度来看，在一定的时间间隔内，一个离子(称为中心离子)的周围，异性离子出现的机会要比同性离子大，这样，在强电解质溶液中，每个离子的周围相对集中的是异性离子，形成了一个异性离子的氛围，该氛围中异性离子的总电荷在数值上与中心离子的电荷相等。我们称这种异性离子氛围为离子氛。从统计平均的角度来看，在没有外加电场作用时，这种异性离子的氛围是球形对称的。每个离子都可作为中心离子而被异性离子包围，同时，每个离子又可成为另一个或若干个异性中心离子的离子氛的一员。由于离子的热运动使离子在溶液中所处的位置经常发生变化，因此离子氛是瞬息万变的。
有了离子氛的模型，就可以将强电解质溶液中离子间的静电作用形象地当作中心离子与其离子氛之间的作用，使所研究的问题大大简化。
在无限稀释的电解质溶液中，离子间的距离很大，离子间的引力可忽略不计，离子的运动就不受其它离子的影响，此时，溶液的性质与理想溶液一样。而在真实的电解质溶液中，由于离子氛的存在而影响离子的行动，表现出偏离理想溶液的性质。因此，在一定的温度、压力、浓度的条件下，若将真实的电解质溶液变成理想溶液，则相当于将中心离子与离子氛拆散，使溶液中的离子间不发生静电吸引作用，这显然需要作非体积功，故在相同的温度、压力及浓度下，真实的电解质溶液的化学势不同于理想溶液的化学势，两者之差就是真实电解质溶液非理想化的原因所在。德拜－休克尔从这个差值出发，在理论上推导出真实电解质溶液中i离子的活度因子公式为
(41a)
该公式称为德拜－休克尔极限定律。之所以称之为极限定律，是因为公式推导过程中的一些假定只有在溶液非常稀时才成立，一般在0.01
以下公式才适用。式中，i为溶液中的任一离子，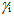
为i离子的活度因子，zi为i离子的电荷数，A在一定的温度下对指定溶剂为一常数，例如，298.15K的水溶液中A=0.509
－1/2。
由于单个离子无法存在，其活度因子不能直接由实验测得，因此必须将式(41a)变成可测量的离子平均活度因子
的形式。根据
与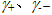
的关系式(36)，并考虑到电解质溶液的电中性条件
,可得
即 
(41b)
上式也是德拜－休克尔极限公式，适用范围同于式(41a)。
例8 在298.15K时，某溶液含CaCl2的浓度为0.002 mol·kg-1，ZnSO4的浓度亦为0.002 mol·kg-1。试用德拜—休克尔极限公式求ZnSO4的离子平均活度因子。
解 在计算离子强度时要把溶液中的所有离子都考虑进去，即
I = 1/2×(2×0.002×12＋0.002×22＋0.002×22＋0.002×22)mol·kg-1
= 0.014mol·kg-1
=－0.509×2×2×(0.014)1/2
=－0.2409
=0.574
请同学们继续学习
