一、 基本内容
电解质溶液属第二类导体，它之所以能导电，是因为其中含有能导电的阴、阳离子。若通电于电解质溶液，则溶液中的阳离子向阴极移动，阴离子向阳极移动；同时在电极/溶液的界面上必然发生氧化或还原作用，即阳极上发生氧化作用，阴极上发生还原作用。法拉第定律表明，电极上起作用的物质的量与通入的电量成正比。若通电于几个串联的电解池，则各个电解池的每个电极上起作用的物质的量相同。
电解质溶液的导电行为，可以用离子迁移速率、离子电迁移率(即淌度)、离子迁移数、电导、电导率、摩尔电导率和离子摩尔电导率等物理量来定量描述。在无限稀释的电解质溶液中，离子的移动遵循科尔劳乌施离子独立移动定律，该定律可用来求算无限稀释的电解质溶液的摩尔电导率。此外，在浓度极稀的强电解质溶液中，其摩尔电导率与浓度的平方根成线性关系，据此，可用外推法求算无限稀释时强电解质溶液的极限摩尔电导率。
为了描述电解质溶液偏离理想稀溶液的行为，以及解决溶液中单个离子的性质无法用实验测定的困难，引入了离子强度、离子平均活度、离子平均质量摩尔浓度和平均活度因子等概念。对稀溶液，活度因子的值可以用德拜－休克尔极限定律进行理论计算，活度因子的实验值可以用下一章中的电动势法测得。
二、 重点与难点
1．法拉第定律：
，式中法拉第常量F=96485 C·mol-1。若欲从含有Mz+离子的溶液中沉积出M，则当通过的电量为Q时，可以沉积出的金属M的物质的量n为：
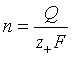，更多地将该式写作
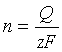，所沉积出的金属的质量为：
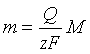，式中M为金属的摩尔质量。
2．离子B的迁移数：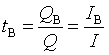
，
3．电导：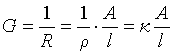
(k为电导率，单位：S·m-1)
电导池常数：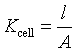
4．摩尔电导率：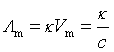
(c：电解质溶液的物质的量浓度, 单位：mol·m-3, 
的单位：
)
5．科尔劳乌施经验式：
6．离子独立移动定律：在无限稀释的电解质
溶液中，
,式中，
、
分别为阳离子、阴离子的化学计量数。
7．奥斯特瓦尔德稀释定律：设
为弱电解质
浓度为c时的摩尔电导率，
为该电解质的极限摩尔电导率，则该弱电解质的解离度为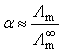
若弱电解质为1-1价型或2-2价型，则此时弱电解质化学式为
，其解离平衡常数为：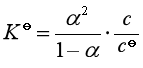
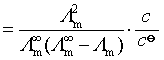
该式称为奥斯特瓦尔德稀释定律。
8．电解质
的溶液中的离子平均质量摩尔浓度
和离子平均活度因子
：
，
式中，
9．电解质
的溶液中阴、阳离子的活度：
，
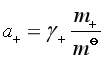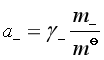
10．电解质B(
)的溶液的活度aB及离子平均活度
：
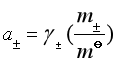
11．离子强度：
12．德拜－休克尔极限公式：
(I<0.01mol·kg－1)
(I<0.01mol·kg－1)
进入你问我答
