一、气固吸附及分类

固体表面层的分子与液体表面层分子一样，也具有过剩的自由能，但因固体不具有流动性，所以不能象液体那样用尽量缩小表面积的方法来降低系统的表面吉布斯自由能。但是，固体表面层分子因受力不均而具有剩余力场，能对碰撞到固体表面的气体分子产生吸引力，使气体分子在固体表面上发生相对地聚集，其结果能减少剩余力场，降低固体的表面吉布斯自由能。使具有较大表面的固体系统变得较为稳定。这种气体分子在固体表面上聚集的现象，称为气体在固体表面上的吸附，简称气固吸附。吸附气体的固体叫做吸附剂，被吸附的气体叫做吸附质。

有关气固吸附的知识，在生产实践和科学实验中应用非常广泛，例如复相催化作用，色层分析方法，气体的分离与纯化，废气中有用成分的回收等，都与气固吸附现象有关。

按照吸附时固体表面分子对所吸附气体分子的作用力的性质，将气固吸附区分为物理吸附和化学吸附。

物理吸附：固体表面分子与气体分子间的吸附力是范德华引力。因气体分子凝聚为液体的力也是范德华引力，所以，物理吸附类似于气体在固体表面上的凝聚。

化学吸附：固体表面分子与气体分子间的吸附力是化学键，吸附过程中可以有电子的转移，原子的重排，化学键的破坏与形成等。所以，化学吸附类似于气体分子与固体表面分子发生化学反应。

正是因为这两类吸附的作用力性质上的不同，引起了两类吸附在特征上的一系列差别，现将其中几项主要差别列于表7：

表7 物理吸附与化学吸附的比较

	物  理  吸  附	化  学  吸  附
吸    附    力	范  德  华  力	化  学  键  力
吸    附    热	较小，近于液化热	较大，近于化学反应热
吸 附 选 择 性	无  选  择  性	有  选  择  性
吸 附 稳 定 性	不稳定，易解吸	比较稳定，不易解吸
吸 附 分 子 层	单分子层或多分子层	单分子层
吸  附  速  率	较快，且不受温度影响	较慢，温度升高速率加快

这两类吸附有时可能同时发生，例如氧在金属钨上的吸附，被吸附的氧有的呈分子状态（物理吸附），有的呈原子状态（化学吸附）。有些吸附系统，低温时发生物理吸附，高温时发生化学吸附，例如氢在镍上的吸附就是如此。

二、吸附平衡与吸附量

气相中的分子可以被吸附在固体表面上，已被吸附的气体分子也可以脱附（或解吸）而逸回气相。固定温度及吸附质的分压之后，当吸附速率与脱附速率相等，即单位时间内被吸附的气体量与脱附的气体量相等时，达到吸附平衡状态，此时吸附在固体表面上的气体量不再随时间而变化。

在达到吸附平衡的条件下，每克吸附剂所能吸附的气体的物质的量(x)或这些气体在标准状况下所占的体积(V)，称为吸附量q，即

          或              （46）

其中m为吸附剂的克数。吸附量可以用实验方法直接测定。

三、吸附曲线

实验表明，对于指定的吸附剂和吸附质来说，吸附量q与吸附温度T及吸附质的分压p有关，即q=f(T,p)。在q、T、p这三个量中，固定其中之一，而反映另外两个量的关系的曲线，称为吸附曲线。显然，吸附曲线有三种：

1. 吸附等温线：指定温度下，反映吸附量与吸附质平衡分压的关系曲线，即一 定T下的q=f(p)曲线。常见的吸附等温线有五种类型，如图22。

  

图22 五种类型的吸附等温线

室温下氨、氯乙烷等在炭上的吸附及低温下氮在细孔硅胶上的吸附常表现为第Ⅰ种类型；﹣78℃下CO₂在硅胶上及室温下水蒸气在粗孔硅胶上的吸附常表现为第Ⅱ类吸附曲线；低温下溴在硅胶上的吸附属于第Ⅲ种类型；室温下苯蒸气在氧化铁凝胶或硅胶上的吸附属于第四种；100℃下水蒸气在活性炭上的吸附等温线为第Ⅴ种类型。  

2. 吸附等量线：规定吸附量的条件下，反映吸附温度与吸附质平衡分压关系的曲线，即q一定时p=f(T)曲线。图23为物理吸附的等量线。 若将吸附平衡表示如下：

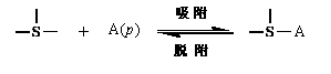
则 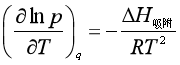                   （47）

由于吸附是自发变化，所以ΔG＜0，又气体分子被吸附后混乱度降低，故ΔS＜0，根据热力学关系式ΔG=ΔH-TΔS可知，ΔH吸附一般为负值，即吸附过程放热。

若已知等量线，便可由曲线斜率求得吸附热．

3. 吸附等压线：指定吸附质平衡分压的情况下，反映吸附量与吸附温度之间关系的曲线，即p一定时，q=f(T)曲线。由于吸附过程放热，所以温度升高时吸附量应降低．物理吸附因速率快，易达到平衡，所以实验中确能表现出吸附量随温度升高。

而下降的规律（图24）。但是，化学吸附因速率较慢，温度低时，常常在一定时间内不能达到吸附平衡，而升温会使吸附速率加快，此时会出现吸附量随温度升高而增加的情况，直到真正达到平衡后，吸附量又随温度升高而下降（图25）。
  

   

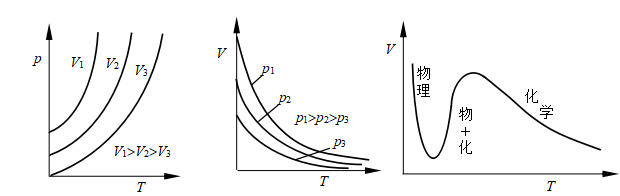
由于物理吸附与化学吸附等压线的形状不同，故可以利用等压线来判断吸附的类型。

四、朗格缪尔单分子层吸附等温式

1916年，朗格缪尔(Langmuir)根据分子间力随距离的七次方而迅速下降的事实，提出了吸附只限制在单分子层的理论，这一理论对于化学吸附和高温低压时的物理吸附获得了很大的成功。

Langmuir理论认为气体分子碰撞到固体表面时有两种可能的情况：一是弹性碰撞，即撞上又立即返回气相；二是非弹性碰撞，即分子在固体表面上停留一段时间后再返回气相，停留时间有长有短，视吸附力的强弱而定。Langmuir认为气体分子在固体表面上的停留就是吸附现象，当吸附达到平衡后，单位时间碰撞到固体表面的分子数与由表面逸出的分子数相等，即吸附速率等于脱附速率。在具体推导吸附方程式时，Langmuir提出了三点假设：(1)只有碰撞到空白表面的气体分子才可能被吸附，而碰撞到已被吸附的分子上时，则是弹性碰撞，即只发生单分子层吸附。(2)气体分子被吸附的概率和被吸附的气体分子离开表面回到气相的概率相等，不受邻近有无吸附分子的影响，即吸附分子间无相互作用。(3)气体分子被吸附在表面的任何位置 ，所放出的吸附热都相同，即固体表面是均匀的。在以上三点假设的基础上，推导出了Langmuir吸附等温式。

设q为一定温度下固体表面被复盖的百分数，则（1-θ）代表空白表面的百分数。根据假设(1)，吸附速率r吸附应正比于（1-θ），此外，r吸附还应与气体的平衡压力p成正比。写成等式则为

         

k₁是比例常数。根据假设(2)，脱附速率应与θ成正比，即

         

达到吸附平衡时，r吸附=r脱附，即

         

整理后得

                      (48)

其中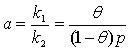，称之为吸附平衡常数或吸附系数。a值越大，表示固体表面对气体吸附的能力越强。
气体在固体表面的吸附量q与θ成正比，θ的大小就代表了吸附量的多少，所以式(48)即为Langmuir吸附等温式。由此式可知：

(1) p很小时，ap<<1，则，即低压下吸附量与气体平衡压力成正比。

(2) p很大时,ap>>1，则θ=1，此时气体在固体表面铺满单分子层，达到饱和吸附状态，吸附量为一常数V_m。

利用式(48)作图，得到的是图22中的第I类吸附等温线。

若以V_m和V分别表示饱和吸附时和气体的分压为p时气体的标准状况体积，则

        

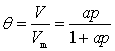
整理后可得

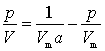                         （49）

式(49)为用饱和吸附量表示的Langmuir吸附等温式。若以p/V对p作图，应得一直线，斜率为-1/V_m，截距为1/V_m，由直线的斜率和截距可求得和V_m。

Langmuir等温式是一个理想的吸附公式，它描述了在均匀表面，吸附分子间无相互作用，吸附为单分子层的情况下达吸附平衡时的吸附规律，它在吸附理论中所起的作用类似于理想气体状态方程在气体运动论中的作用。人们往往以它作为一个基本公式，先考虑理想情况，找出某些规律性，然后针对具体系统对这些规律予以修正。

五、多分子层吸附等温式

Langmuir单分子层吸附理论推导出的吸附等温式，只适用于第Ⅰ类吸附等温线，而对于第Ⅱ至Ⅴ类吸附等温线都不能给予解释，1938年，勃劳纳尔-爱密特-泰勒(Brunnauer-Emmett-Teller)三人提出了多分子层的气固吸附理论的公式，简称BET公式。这个理论是在Langmuir理论的基础上发展而得到的，他们接受了Langmuir理论中关于吸附作用是吸附与脱附平衡的概念，接受了Langmuir理论中关于固体表面是均匀的，吸附分子间无相互作用的假设。同时，他们又认为固体表面吸附了一层分子之后，由于气体分子本身的范德华引力，还可以继续发生多分子层吸附。但是，第一层的吸附与以后各层的吸附有本质的区别，前者是气体分子与固体表面直接发生联系，而后者则是相同分子之间的相互作用。第一层的吸附热也与以后各层不同，而第二层以后各层的吸附热都相同，而且近似于气体的凝聚热。当吸附达到平衡后，吸附量等于各层吸附量的总和。在此基础上导出的吸附等温式为

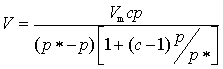                （50）

此即BET公式。式中V与V_m分别是气体在分压为p达吸附平衡时和固体表面铺满单分子层时被吸附气体在标准状况下的体积，p^*是实验温度下气体的饱和蒸气压，C是与吸附热有关的常数。

式(50)可整理成下列形式

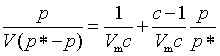                 （51）

以p/V(p^*-p)对p/p^*作图，应得一直线，由直线的斜率和截距可以求得V_m和C，其中

若已知被吸附分子的截面积，则可以由V_m计算出固体吸附剂的比表面积a_s：

                          （52）

式中S为一个吸附质分子的横截面积，是固体吸附剂的质量，L为阿佛加德罗常量。利用BET公式测定固体比表面的方法被认为是目前测定比表面的简单而且准确的方法。

BET公式能适用于单分子层和多分子层吸附，能对Ⅰ、Ⅱ、Ⅲ三种类型的吸附等温线给予说明。大量事实表明，当相对压力（p/p^*）在0.05-0.35范围内，大多数吸附系统的实验结果能符合BET理论。因而BET理论是目前最成功的物理吸附理论。

但是，BET理论仍假设固体表面是均匀的，而实际上固体表面是粗糙的、不均匀的，表面各处的吸附能力是不同的，吸附热也有很大差别。另外，BET理论仍假设被吸附分子间无相互作用，但却认为上下层分子间的范德华力引起多分子层吸附，这一观点也是难以令人接受的。所以BET理论不能对第Ⅳ类和第Ⅴ类等温线给予解释，并且只在一定的压力范围内与实验事实相符。

一般认为，当相对压力小于0.05时，由于压力太小，建立不起来多分子层吸附平衡，甚至连单分子层的物理吸附也远未完全形成，此时表面的不均匀性就显得突出了，因而与BET公式产生偏差。当相对压力大于0.35时，可能因为毛细管凝聚，破坏了多分子层吸附平衡而偏离BET公式。

BET理论的局限，说明吸附理论有待进一步发展，以适应生产和科研的需要。