2.6 数值微分

作为多项式插值的直接应用，本节介绍两种求函数导数近似值的方法。

2.6.1 利用插值多项式求导数的原理与常用公式

若函数在节点处的函数值已知，就可作的次插值多项式，并用近似代替，即

由于是多项式，容易求导数，故对应于的每一个插值多项式，就易建立一个数值微分公式

                               (2.6.1)

这样建立起来的数值微分公式，统称为插值型微分公式。

必须注意，即使与的近似程度非常好，导数与在某些点上的差别仍旧可能很大。因而，在应用数值微分公式时，要重视对误差的分析。

由插值余项公式(2.2.9)知

            (2.6.2)

由于式中是的未知函数，故时，无法利用上式对误差作出估计。但是，如果我们限定求某个节点处的导数值，那么式(2.6.2)右端第二项之值应为零，此时有

若将它写成带余项的数值微分公式，即

                       （2.6.3）

其中，在之间。该式右端由两部分，即导数的近似值和相应的截断误差组成。

作为特例，当时，插值节点为，若记，则由式(2.6.3)得带余项的两点公式

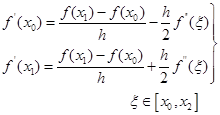                       （2.6.4）

前一公式的实质是用在处的向前差商（分子是向前差分的差商）作为的近似值，后一公式则是用

在处的向后差商（分子是向后差分的差商）作为的近似值。

当且节点为时，由式(2.6.3)可得带余项的三点公式

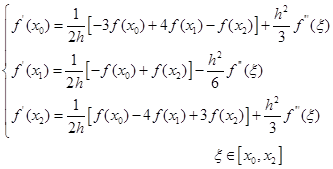              （2.6.5）

中间一个公式的实质是用在处的中心差商作为的近似值，与前、后两公式相比较，其优越性是显然的。

用插值多项式作为的近似函数，还可用来建立高阶的数值微分公式，例如，带余项的二阶三点公式

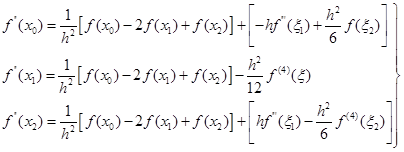       （2.6.6）

2.6.2 利用三次样条插值函数求导数的原理与公式

由§5知，对于给定函数表

和适当的边界条件，我们可以写出三次样条插值函数，并用近似代替，即

由于是一个分段三次多项式，在各子区间上容易求出导数，故可建立数值微分公式

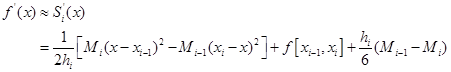     (2.6.7)

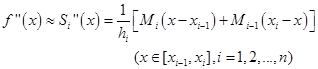             (2.6.8)

 

例8利用函数在节点上的函数值和边界条件

构造三次样条插值函数，并用它来计算和在下列点

处的近似值。部分计算结果如表2-5所示。

表2-5

由表2-5可以看出，利用三次样条插值函数及其导数来逼近被插值函数及其导数，其效果是相当好的。