本章导入：

在某个实际问题中，虽然可以断定所考虑的函数在区间上存在且连续，但却难以找到它的解析表达式，只能通过实验和观测得到在有限个点上的函数值（即一张函数表）。

（1）要利用这张函数表来分析函数的性态，甚至直接求出其他一些点上的函数值可能是非常困难的。

（2）虽然写出函数的解析表达式，但由于结构相当复杂，使用起来很不方便。

（3）根据所得函数表（或结构复杂的解析表达式），构造某个简单函数作为的近似。

插值法是解决此类问题的一种比较古老的、然而却是目前常用的方法，它不仅直接广泛地应用于生产实际和科学研究中，而且也是进一步学习数值计算方法的基础。

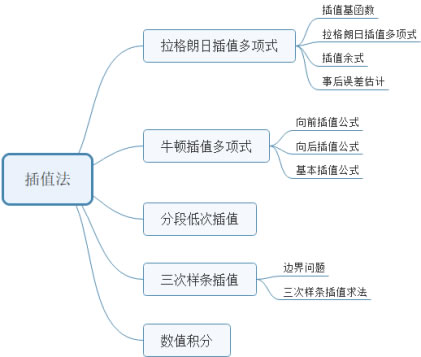
学习目标：

（1）学习多项式插值的概念，插值多项式的存在唯一性；

（2）掌握拉格朗日插值多项式；

（3）掌握牛顿插值多项式；

（4）了解分段低次插值;

（5）了解三次样条插值;

（6）了解数值微分。

知识结构