本章练习答案
1.确定一个具有3次代数精度的求积公式
![]()
解:由代数精度的定义,将![]() 分别代入公式得:
分别代入公式得:
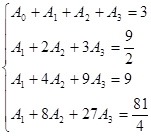 解得:
解得: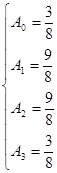 ,
,
该求积公式为:
![]() 。
。
2.熟练掌握插值型求积公式![]() 中求积系数
中求积系数![]() 的求法。
的求法。
解:![]()
![]()
3.用辛普生公式计算积分![]() ,并估计截断误差。
,并估计截断误差。
解:设![]() ,
,![]() ;
;
![]()
由辛普生公式有:
![]()
其截断误差为:![]()
![]() 。
。
4.用定义确定求积公式![]() 中的待定系数
中的待定系数![]() ,并指出该公式的代数精度。
,并指出该公式的代数精度。
解:由插值型求积公式可知:
![]()
所以:![]() ;
;
![]() ;
;
![]() 。
。
将![]() 代入公式两边得:左边=
代入公式两边得:左边=![]() =右边;
=右边;
将![]() 代入公式两边得:左边=
代入公式两边得:左边=![]() =右边;
=右边;
将![]() 代入公式两边得:左边=
代入公式两边得:左边=![]() =右边;
=右边;
将![]() 代入公式两边得:左边=
代入公式两边得:左边=![]() =右边;
=右边;
将![]() 代入公式两边得:左边=
代入公式两边得:左边=![]() 右边
右边![]() 。
。
所以该公式具有3次代数精度。
5.确定求积公式![]() 中的代数系数,使其代数精度尽量高,并指明所构造出的求积公式所具有的代数精度。
中的代数系数,使其代数精度尽量高,并指明所构造出的求积公式所具有的代数精度。
解:将![]() 分别代入公式得:
分别代入公式得:
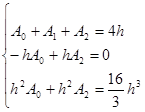 解得:
解得: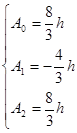 ,该求积公式为:
,该求积公式为:
![]()
该公式对![]() 成立,但对
成立,但对![]() 不成立。所以该公式的代数精度为3次。
不成立。所以该公式的代数精度为3次。
6.用柯特斯系数![]() 的定义式,计算四点求积公式中的柯特斯系数
的定义式,计算四点求积公式中的柯特斯系数![]() ,并写出四点求积公式
,并写出四点求积公式![]() 。
。
解:由![]() 可得:
可得:
![]() ;
;
![]() ;
;
![]() ;
;
![]() 。
。
7.应用梯形公式和![]() 的复合梯形公式计算积分
的复合梯形公式计算积分![]() ,并估计误差。
,并估计误差。
解:由梯形公式![]() 可得:
可得:
![]() ;
;
余项为: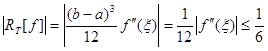
由![]() ,可得:
,可得:![]() ,由复合梯形公式
,由复合梯形公式![]() ,可得:
,可得:
![]() ;
;
余项为: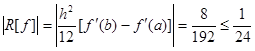 。
。
8.在用复合梯形公式![]() 计算
计算![]() 时,若要求误差不超过
时,若要求误差不超过![]() ,
,![]() 至少去多大?
至少去多大?
解:由复合梯形公式的余项公式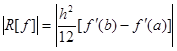 得,用该公式计算
得,用该公式计算![]() 的误差为:
的误差为:
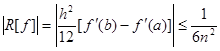 ,所以当
,所以当![]() 时,误差不超过
时,误差不超过![]() 。
。
9.用![]() 的复合辛普生公式计算
的复合辛普生公式计算![]() ,并作事后误差估计。
,并作事后误差估计。
解:由![]() 可得,
可得,![]() ,所以各节点为:
,所以各节点为:![]()
![]() ,所以
,所以![]() ,其余项为
,其余项为
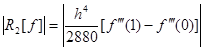 。
。
10.熟悉用变步长梯形公式求积分![]() 以及龙贝格公式
以及龙贝格公式![]() 的计算过程。
的计算过程。
解:变步长求积公式:![]() ,
,![]()
龙贝格算法的计算过程为:
(1)计算![]() ,
,![]() 和
和![]() ;
;
(2)将区间![]() 分半,计算
分半,计算![]() ,
,![]() 和
和![]() ;
;
(3)分别将区间![]() ,
,![]() 分半,计算
分半,计算![]() ,
,![]() ,
,
![]() ,
,![]() ,进而计算
,进而计算![]() ;
;
(4)又将区间![]() ,
,![]() ,
,![]() ,
,![]() 分半,计算
分半,计算![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,进而计算
,进而计算![]() 。
。
(5)继续将上述小区间分半,计算出分点处的函数值,并分别计算出![]()
如此反复可得![]() ,直到前后两个
,直到前后两个![]() 的值之差满足给定的精度要求为止。
的值之差满足给定的精度要求为止。
11.已知积分![]() ,为保证积分有5位有效数字,问:
,为保证积分有5位有效数字,问:
(1)在使用复合梯形公式计算![]() 时,
时,![]() 至少取多大?
至少取多大?
(2)在使用辛普生公式计算![]() 时,
时,![]() 至少去多大?
至少去多大?
解:由![]() ,所以由积分有5位有效数字可得积分的相对误差限为
,所以由积分有5位有效数字可得积分的相对误差限为
![]() 。
。
(1)由复合梯形公式的余项![]() 可得,要达到误差要求即
可得,要达到误差要求即
![]() ,解得
,解得![]() 至少取54。
至少取54。
(2)由复合辛普生公式的余项![]() 可得,要达到误差要求即
可得,要达到误差要求即
![]() ,解得
,解得![]() 至少取2。
至少取2。
12.试构造两点高斯公式![]() ,并由此计算积分
,并由此计算积分![]() 。
。
解:由2次勒让德多项式![]() 可得,
可得,![]() ,
,![]() 即为高斯点。再由
即为高斯点。再由
![]() 得
得![]() 。所以两点高斯公式为:
。所以两点高斯公式为: ![]() 。
。
令![]() ,当
,当![]() 时
时![]() ,当
,当![]() 时
时![]() ,
,![]() ,于是
,于是![]()
![]()