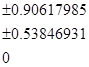知识点四：高斯型求积公式
4.4 高斯型求积公式
本节简要介绍一种高精度的求积公式----高斯（Gauss）型求积公式。
4.4.1 高斯型求积公式的定义
在4.2节中，我们限定吧把积分区间的等分点作为求积节点，从而构造出一类特殊的插值型求积公式，即牛顿—柯特斯公式。这种做法虽然简化了计算，但却降低了所得公式的代数精度。例如，在构造形如
(4.4.1)
的两点公式时，如果限定求积节点
那么所得插值型求积公式
(4.4.2)
的代数精度仅为1。但是，如果我们对式（4.4.1）中的系数
和节点
都不加限制，那么就可以适当选取
和
，使所的公式的代数精度
。事实上，若要求求积公式（4.4.1）对函数
都准确成立，只要
和
满足方程组
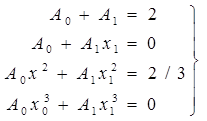(4.4.3)
解之得
代入式（4.4.1）即得
(4.4.4)
容易验证，所得公式（4.4.4）是代数精度
的插值型求积公式。
同理，对于一般求积公式
(4.4.5)
只要适当选择2
+2个待定参数
和
要使它的代数精度达到
也是完全可能的。
定义3 若形如式（4.4.5）的求积公式代数精度达到了
，则称它为高斯型求积公式，并称相应的求积节点
为高斯点。
可以证明，高斯型求积公式也是插值型的。
4.4.2 高斯型求积公式的构造与应用
我们可以像构造两点高斯型求积公式（4.4.4）那样，通过解一个形如（4.4.3）的方程组来确定高斯点
和求积系数
从而构造
点高斯型求积公式。但是，这种做法要解一个包含有
个未知数的非线性方程组，其计算工作量是相当大的。一个比较简单的方法是：
（1）先利用区间
上的
次正交多项是确定高斯点
。
(2)然后利用高斯点确定求积系数
。
限于学时，在本书中对这个方法的理论依据与具体做法均不作介绍，需要了解的读者可查阅参考文献[1]。
下面，我们给出当积分区分是
时，两点至五点高斯型求积公式的节点、系数和余项（见表4-6,其中
），需要时可查用。
利用表4-6，可以方便地写出相应的高斯型求积公式。例如，当
时，由表4-6知
故得两点高斯型求积公式
表4-6
节点数 |
节点 |
系数 |
余额R[f] |
2 |
|
1 |
|
3 |
|
0.55555556 0.88888889 |
|
4 |
|
0.34785485 0.65214515 |
|
5 |
|
0.23692689 0.47862867 0.58888889 |
|
又如，当
时，由表4-6可以查出三个求积节点和对应的三个系数（注意：系数0.55555556应连用两次），从而得到三点高斯型求积公式
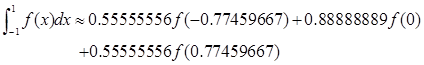
对与一般区间
上的积分，我们也可以利用表4-6写出高斯型求积公式。其原理与方法是：先作变量替换，令
将区间
上的积分转化为区间
上的积分
（4.4.6）
记
则等式（4.4.6）右端的积分就是
。利用表4-6，对于给定的
，可以写出高斯型求积公式
（4.4.7）
即
代入式（4.4.6）得
（4.4.8）
其中，系数
与节点
可在表4-6中查得。由变量替换式
容易看出，由于求积公式(4.4.7)对变量
不高于
次的多项式准确成立，从而求积公式(4.4.8)对变量
不高于
次的多项式也准确成立，即式（4.4.8）是高斯型求积公式。
例4 利用四点高斯型求积公式计算
的近似值。
解 由表4-6和高斯型求积公式（4.4.8）得
①
其中
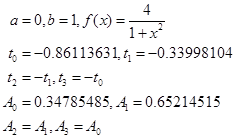
将各数及已知函数
带入①进行计算，即得
在例4的整个计算过程中，只涉及到求四个点上的函数值。可见高斯型求积公式具有工作量小、所得近似值精确程度高等优点，是一种高精度的求积公式。
高斯型求积公式的明显缺点是，但
改变大小时，系数和节点几乎都在改变。我们虽然可以通过其他资料查到较大
时的系数和节点，但应用时却十分不便。同时，由表4-6给出的余项，其表达式都涉及被积函数的高阶导数，要利用它们来控制精度也是十分困难的。为了克服这些缺点，在实际计算中较多地采用复合求积的方法。例如，先把积分区间
分成
个等长的小区间
，然后在每个小区间上使用同一低阶（例如两点的、三点的……）高斯型求积公式算出积分的近似值，将它们相加即得积分
的近似值
（4.4.9）
其中，
，
与
由表4-6查得。同时，在实际计算时，还常用相邻两次计算结果
与
的关系式
（4.4.10）
来控制运算（当
时⊿相当于绝对误差，当
时⊿相当于相对误差），即在算出
和
后，观察不等式
（
为指定的精确度）
是否满足。若满足此不等式，则停止运算，并把
取作待求的积分近似值，否则计算
，并观察不等式
是否满足……直到得到满足精度要求的近似值为止。
进入知识归纳
